Intermediate engineering analysis/Problem set 2

Problem R2.1

Part 1

Problem Statement

Given the two roots and the initial conditions:

$\lambda _{1}=-2,\lambda _{2}=5\!$
$y(0)=1,y'(0)=0\!$

Find the non-homogeneous L2-ODE-CC in standard form and the solution in terms of the initial conditions and the general excitation $r(x)\!$.
Consider no excitation:
$r(x)=0\!$
Plot the solution

Solution

Characteristic Equation:

$(\lambda -\lambda _{1})(\lambda -\lambda _{2})=0\!$
$(\lambda +2)(\lambda -5)=\lambda ^{2}+2\lambda -5\lambda -10=0\!$

 $\lambda ^{2}-3\lambda -10=0\!$

Non-Homogeneous L2-ODE-CC

 $y''-3y'-10=r(x)\!$

Homogeneous Solution:

$y_{h}(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!$
$y(x)=c_{1}e^{-2x}+c_{2}e^{5x}+y_{p}(x)\!$
Since there is no excitation,
$y_{p}(x)=0\!$

 $y(x)=c_{1}e^{-2x}+c_{2}e^{5x}\!$

Substituting the given initial conditions:

$y(0)=1\!$

 $1=c_{1}+c_{2}\!$

$y'(0)=0\!$

 $0=-2c_{1}+5c_{2}\!$

Solving these two equations for $c_{1}\!$ and $c_{2}\!$ yields:

 $c_{1}=5/4,c_{2}=-1/4\!$

Final Solution

 $y(x)=(5/4)e^{-2x}-(1/4)e^{5x}\!$

Part 2

Problem Statement

Generate 3 non-standard (and non-homogeneous) L2-ODE-CC that admit the 2 values in (3a) p.3-7 as the 2 roots of the corresponding characteristic equation.

Solutions

$2(\lambda +2)(\lambda -5)=2\lambda ^{2}+4\lambda -10\lambda -20=0\!$

 $2\lambda ^{2}-6\lambda -20=0\!$

$3(\lambda +2)(\lambda -5)=3\lambda ^{2}+6\lambda -15\lambda -30=0\!$

 $3\lambda ^{2}-9\lambda -30=0\!$

$4(\lambda +2)(\lambda -5)=4\lambda ^{2}+8\lambda -20\lambda -40=0\!$

 $4\lambda ^{2}-12\lambda -40=0\!$

--Egm4313.s12.team11.gooding 02:01, 7 February 2012 (UTC)

Report 2, Problem 2

Problem Statement

Find and plot the solution for the homogeneous L2-ODE-CC

$y''(x)-10y'(x)+25y(x)=0\!$

with initial conditions $y(0)=1\!$ ,and $y'(0)=0\!$

Characteristic Equation

$\lambda ^{2}-10\lambda +25=0\!$

$(\lambda -5)(\lambda -5)=0\!$

$\lambda =5\!$

Homogeneous Solution

The solution to a L2-ODE-CC with real double root is given by

$y(x)=c_{1}e^{\lambda x}+c_{2}xe^{\lambda x}\!$

First initial condition

$y(0)=1\!$

$y(0)=c_{1}e^{5*0}+c_{2}*0*e^{5*0}=1\!$

$c_{1}=1\!$

Second initial condition

$y'(0)=0\!$

${\frac {d}{dx}}y(x)=y'(x)=5e^{5x}+c_{2}e^{5x}(5x+1)\!$

$y'(0)=5e^{5*0}+c_{2}e^{5*0}(5*0+1)=0\!$

$5+c_{2}=0\!$

$c_{2}=-5\!$

The solution to our L2-ODE-CC is

                       $y(x)=e^{5x}(1-5x)\!$

Plot

$y(x)=e^{5x}(1-5x)\!$

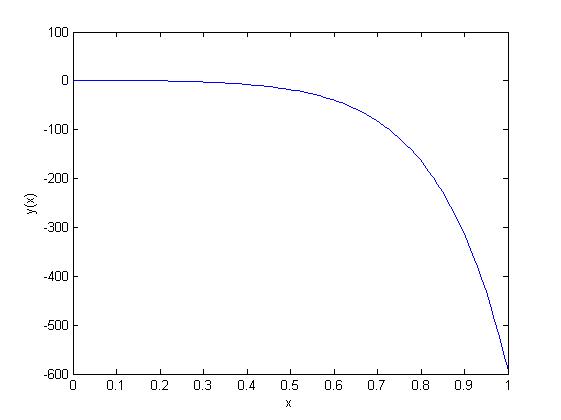
Egm4313.s12.team11.imponenti 00:30, 8 February 2012 (UTC)

Problem R2.3

Problem Statement (K 2011 p.59 pb. 3)

Find a general solution. Check your answer by substitution.

Given

$y''+6y'+8.96y=0\!$

Solution

We can write the above differential equation in the following form:

${\frac {d^{2}y}{dx^{2}}}+6{\frac {dy}{dx}}+8.96y=0$

Let ${\frac {d}{dx}}=\lambda .$

The characteristic equation of the given DE is

$\lambda ^{2}+6\lambda +8.96=0\!$

Now, in order to solve for $\lambda$, we can use the quadratic formula:

$\lambda ={\frac {-(6)\pm {\sqrt {(6)^{2}-4(1)(8.96)}}}{2(1)}}$

$\lambda ={\frac {-6\pm {\sqrt {36-35.84}}}{2}}$

$\lambda ={\frac {-6\pm {\sqrt {0.16}}}{2}}$

$\lambda ={\frac {-6\pm 0.4}{2}}$

Therefore, we have:

$\lambda _{1}={\frac {-6+0.4}{2}}={\frac {-5.8}{2}}=-2.8$

and

$\lambda _{1}={\frac {-6-0.4}{2}}={\frac {-6.4}{2}}=-3.2$

Thus, we have found that the general solution of the DE is actually:

$y=c_{1}e^{-2.8x}+c_{2}e^{-3.2x}\!$

Check:

To check if $y$ is indeed the solution of the given DE, we can differentiate the

what we found to be the general solution.

${\frac {dy}{dx}}=y'=-2.8xc_{1}e^{-2.8x}+-3.2xc_{2}e^{-3.2x}\!$

${\frac {d^{2}y}{dx^{2}}}=y''=7.84xc_{1}e^{-2.8x}+10.24c_{2}e^{-3.2x}\!$

Substituting the values of $y,y'$ and $y''$ in the given equation, we get:

$7.84c_{1}e^{-2.8x}+10.24c_{2}e^{-3.2x}+6(-2.8c_{1}e^{-2.8x}-3.2c_{2}e^{-3.2x})+8.96(c_{1}e^{-2.8x}+c_{2}e^{-3.2x})=0\!$

$7.84c_{1}e^{-2.8x}+10.24c_{2}e^{-3.2x}-16.8c_{1}e^{-2.8x}-19.2c_{2}e^{-3.2x}+8.96c_{1}e^{-2.8x}+8.96c_{2}e^{-3.2x}=0\!$

and thus:

$0\equiv 0.\!$

Therefore, the solution of the given DE is in fact:

$y=c_{1}e^{-2.8x}+c_{2}e^{-3.2x}\!$

Problem Statement (K 2011 p.59 pb. 4)

Find a general solution to the given ODE. Check your answer by substituting into the original equation.

Given

${y}''+4{y}'+(\pi ^{2}+4)y=0\!$

Solution

The characteristic equation of this ODE is therefore:

$\lambda ^{2}+a\lambda +b=\lambda ^{2}+4\lambda +(\pi ^{2}+4)=0\!$

Evaluating the discriminant:

$a^{2}-4b=4^{2}-4(\pi ^{2}+4)=-4\pi ^{2}<0\!$

Therefore the equation has two complex conjugate roots and a general homogenous solution of the form:

$y=e^{-ax/2}(Acos(\omega x)+Bsin(\omega x))\!$

Where: $\omega ={\sqrt {b-{\frac {1}{4}}a^{2}}}={\sqrt {\pi ^{2}+4-{\frac {1}{4}}(4)^{2}}}={\sqrt {\pi ^{2}}}=\pi \!$

And finally we find the general homogenous solution:

                                                  $y=e^{-2x}(Acos(\pi x)+Bsin(\pi x))\!$

Check:

We found that:

$y=e^{-2x}(Acos(\pi x)+Bsin(\pi x))\!$

Differentiating $y\!$ to obtain ${y}'\!$ and ${y}''\!$ respectively:

${y}'=-2e^{-2x}(Acos(\pi x)+Bsin(\pi x))+e^{-2x}(\pi Acos(\pi x)-\pi Bsin(\pi x))\!$

                                   ${y}'=-2e^{-2x}(Acos(\pi x)+Bsin(\pi x))+\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))\!$

${y}''=4e^{-2x}(Acos(\pi x)+Bsin(\pi x))-2\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))-2\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))-\pi ^{2}e^{-2x}(Acos(\pi x)+Bsin(\pi x))\!$

                 ${y}''=4e^{-2x}(Acos(\pi x)+Bsin(\pi x))-4\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))-\pi ^{2}e^{-2x}(Acos(\pi x)+Bsin(\pi x))\!$

Substituting these equations into the original ODE yields:

$4e^{-2x}(Acos(\pi x)+Bsin(\pi x))-4\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))-\pi ^{2}e^{-2x}(Acos(\pi x)+Bsin(\pi x))\!$

$+4(-2e^{-2x}(Acos(\pi x)+Bsin(\pi x))+\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x)))+(\pi ^{2}+4)(e^{-2x}(Acos(\pi x)+Bsin(\pi x)))=0\!$

$4e^{-2x}(Acos(\pi x)+Bsin(\pi x))-4\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))-\pi ^{2}e^{-2x}(Acos(\pi x)+Bsin(\pi x))\!$

$-8e^{-2x}(Acos(\pi x)+Bsin(\pi x))+4\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))+\pi ^{2}e^{-2x}(Acos(\pi x)+Bsin(\pi x))+4e^{-2x}(Acos(\pi x)+Bsin(\pi x))=0\!$

$(4-8+4)e^{-2x}(Acos(\pi x)+Bsin(\pi x))+(-4+4)\pi e^{-2x}(Acos(\pi x)-Bsin(\pi x))+(\pi ^{2}-\pi ^{2})e^{-2x}(Acos(\pi x)+Bsin(\pi x))=0\!$

$0\equiv 0\!$

Therefore, the solution is correct.

--Gonzalo Perez

Problem R2.4

K 2011 p.59 pb. 5

Problem Statement

Find a general solution to the given ODE. Check your answer by substituting into the original equation.

Given

${y}''+2\pi {y}'+\pi ^{2}y=0\!$

Solution

The characteristic equation of this ODE is therefore:

$\lambda ^{2}+a\lambda +b=\lambda ^{2}+2\pi \lambda +\pi ^{2}=0\!$

Evaluating the discriminant:

$a^{2}-4b=(2\pi )^{2}-4(\pi ^{2})=4\pi ^{2}-4\pi ^{2}=0\!$

Therefore the equation has a real double root and a general homogenous solution of the form:

$y=(c_{1}+c_{2}x)e^{-ax/2}\!$

And finally we find the general homogenous solution:

                                                       $y=(c_{1}+c_{2}x)e^{-\pi x}\!$

Checking:

We found that:

$y=(c_{1}+c_{2}x)e^{-\pi x}\!$

Differentiating $y\!$ to obtain ${y}'\!$ and ${y}''\!$ respectively:

                                                  ${y}'=c_{2}e^{-\pi x}-\pi (c_{1}+c_{2}x)e^{-\pi x}\!$

And,

${y}''=-\pi c_{2}e^{-\pi x}-\pi c_{2}e^{-\pi x}+\pi ^{2}(c_{1}+c_{2}x)e^{-\pi x}\!$

                                                 ${y}''=-2\pi c_{2}e^{-\pi x}+\pi ^{2}(c_{1}+c_{2}x)e^{-\pi x}\!$

Substituting these equations into the original ODE yields:

$-2\pi c_{2}e^{-\pi x}+\pi ^{2}(c_{1}+c_{2}x)e^{-\pi x}+2\pi (c_{2}e^{-\pi x}-\pi (c_{1}+c_{2}x)e^{-\pi x})+\pi ^{2}((c_{1}+c_{2}x)e^{-\pi x})=0\!$

$-2\pi c_{2}e^{-\pi x}+\pi ^{2}(c_{1}+c_{2}x)e^{-\pi x}+2\pi c_{2}e^{-\pi x}-2\pi ^{2}(c_{1}+c_{2}x)e^{-\pi x}+\pi ^{2}(c_{1}+c_{2}x)e^{-\pi x}=0\!$

$(-2\pi +2\pi )c_{2}e^{-\pi x}+(\pi ^{2}-2\pi ^{2}+\pi ^{2})(c_{1}+c_{2}x)e^{-\pi x}=0\!$

$0\equiv 0\!$

Therefore this solution is correct.

K 2011 p.59 pb. 6

Problem Statement

Find a general solution to the given ODE. Check your answer by substituting into the original equation.

Given

$10{y}''-32{y}'+25.6y=0\!$

Solution

Initially we modify the original ODE to put it in the form of a second-order homogenous linear ODE with constant coefficients:

$10{y}''-32{y}'+25.6y=0\!$

Dividing both sides by 10:

${y}''-3.2{y}+2.56y=0\!$

The characteristic equation of this ODE is now therefore:

$\lambda ^{2}+a\lambda +b=\lambda ^{2}-3.2\lambda +2.56=0\!$

Evaluating the discriminant:

$a^{2}-4b=(-3.2)^{2}-4(2.56)=10.24-10.24=0\!$

Therefore the equation has a real double root and a general homogenous solution of the form:

$y=(c_{1}+c_{2}x)e^{-ax/2}\!$

And finally we find the general homogenous solution:

                                                       $y=(c_{1}+c_{2}x)e^{1.6x}\!$

Checking:

We found that:

$y=(c_{1}+c_{2}x)e^{1.6x}\!$

Differentiating $y\!$ to obtain ${y}'\!$ and ${y}''\!$ respectively:

                                                  ${y}'=1.6c_{1}e^{1.6x}+c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}\!$

And,

${y}''=(1.6)^{2}c_{1}e^{1.6x}+1.6c_{2}e^{1.6x}+1.6c_{2}e^{1.6x}+(1.6)^{2}c_{2}xe^{1.6x}\!$

                                                 ${y}''=(1.6)^{2}c_{1}e^{1.6x}+3.2c_{2}e^{1.6x}+(1.6)^{2}c_{2}xe^{1.6x}\!$

Substituting these equations into the original ODE yields:

$10[(1.6)^{2}c_{1}e^{1.6x}+3.2c_{2}e^{1.6x}+(1.6)^{2}c_{2}xe^{1.6x}]-32[1.6c_{1}e^{1.6x}+c_{2}e^{1.6x}+1.6c_{2}xe^{1.6x}]+25.6[(c_{1}+c_{2}x)e^{1.6x}]=0\!$

$25.6c_{1}e^{1.6x}+32c_{2}e^{1.6x}+25.6c_{2}xe^{1.6x}-51.2c_{1}e^{1.6x}-32c_{2}e^{1.6x}-51.2c_{2}xe^{1.6x}+25.6c_{1}e^{1.6x}+25.6c_{2}xe^{1.6x}=0\!$

$(25.6-51.2+25.6)c_{1}e^{1.6x}+(32-32)c_{2}e^{1.6x}+(25.6-51.2+25.6)c_{2}xe^{1.6x}=0\!$

$0\equiv 0\!$

Therefore this solution is correct.

Report 2, Problem 2.5

Problem Statement

Problem 2.5 Find an Ordinary Differential Equation. Use $y''+ay'+by=0\!$ for the given basis.

ODE Solutions

Two Real Roots: $y(x)=c_{1}e^{\lambda _{1}x}+c_{2}e^{\lambda _{2}x}\!$
Double Real Roots: $y(x)=c_{1}e^{\lambda _{1}x}+c_{2}xe^{\lambda _{2}x}\!$

Reverse Engineering

$e^{\lambda x}(\lambda ^{2}+a\lambda +b)=0\!$

Case 1: $a^{2}-4b>0\!$
$\lambda ^{2}-(\lambda _{1}+\lambda _{2})\lambda +\lambda _{1}\lambda _{2}\!$
$y''-(\lambda _{1}+\lambda _{2})y'+\lambda _{1}\lambda _{2}y=0\!$

Case 2: $a^{2}-4b=0\!$
$\lambda ^{2}-(\lambda _{1}+\lambda _{2})\lambda +\lambda _{1}\lambda _{2}\!$
$y''-(\lambda _{1}+\lambda _{2})y'+\lambda _{1}\lambda _{2}y=0\!$

Problem Solutions

R2.5 K2011 p.59 pbs.16

$e^{2.6x},e^{-4.3x}\!$
$(\lambda -2.6)(\lambda +4.3)\!$
$\lambda ^{2}+1.7\lambda -11.18\!$

ODE Form:

                                                            $y''+1.7y'-11.18=0\!$

R2.5 K2011 p.59 pbs.17

$e^{-{\sqrt {5}}x},xe^{-{\sqrt {5}}x}\!$
$(\lambda +{\sqrt {5}})^{2}\!$
$\lambda ^{2}+2{\sqrt {5}}\lambda +5\!$

ODE Form:

                                                            $y''+2{\sqrt {5}}y'+5y=0\!$

Created by [Daniel Suh] 20:57, 7 February 2012 (UTC)

Problem 2.6

Solved by: Andrea Vargas

Problem Statement

For the following spring-dashpot-mass system (in series) find the values for the parameters $k,c,m\!$ knowing that the system has the double real root $\lambda =-3\!$

Figure

Solution

Previously, we have derived the following equation for such a system:
(From Sec 1 (d), (3) p.1-5)
$m\left(y_{k}''+{\frac {k}{c}}y_{k}'\right)+ky_{k}=f(t)\!$
We can write this equation in standard form by diving through by $m\!$:
$y_{k}''+{\frac {k}{c}}y_{k}'+{\frac {k}{m}}y_{k}={\frac {f(t)}{m}}\!$
Here, we can take the coefficients of $y_{k}'\!$ and $y_{k}\!$ as $a\!$ and $b\!$:

$y_{k}''+\underbrace {\frac {k}{c}} _{a}y_{k}'+\underbrace {\frac {k}{m}} _{b}y_{k}={\frac {f(t)}{m}}\!$

Next,considering the double real root:
$\lambda =-3\!$
We can find the characteristic equation to be:
$\left(\lambda +3\right)^{2}=\lambda ^{2}+6\lambda +9=0\!$
Which is in the form:
$\lambda ^{2}+a\lambda +b=0\!$

Then, we know that $a=6\!$ and $b=9\!$:

Setting $a\!$ and $b\!$ from the first equation equal to these, we obtain:

                                                             ${\frac {k}{c}}=6\;and\;{\frac {k}{m}}=9\!$

Clearly, there is an infinite amount of solutions to this problem because we have 2 equations but 3 unknowns. This can be solved by fixing one of the values and finding the other two.

Example of Solution

An example of fixing one of the constants to find the other two is provided here. By solving the simple equations above, we can illustrate how to find $k,c,m\!$ . We had:
${\frac {k}{c}}=6\;and\;{\frac {k}{m}}=9\!$

If we fix the mass to $m=10\;kg\!$. We find:
${\frac {k}{10}}=9\!$

$k=90\!$

Then,
${\frac {90}{c}}=6\!$

$c=15\!$

Finally, we obtain:

                                                             $m=10,\;k=90,\;and\;c=15\!$

--Andrea Vargas 21:44, 7 February 2012 (UTC)

Problem 2.7: McLaurin Series

Problem Statement

Develop the McLaurin Series (Taylor Series at t=0) for $e^{t},\cos t,\sin t\!$

Solution

$e^{t}=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}\!$

$={\frac {t^{0}}{0!}}+{\frac {t^{1}}{1!}}+{\frac {t^{2}}{2!}}+{\frac {t^{3}}{3!}}+...{\frac {t^{n}}{n!}}\!$

                                      $e^{t}=1+t+{\frac {t^{2}}{4}}+{\frac {t^{3}}{6}}+...{\frac {t^{n}}{n!}}\!$

$\cos t=\sum _{k=0}^{\infty }{\frac {(-1)^{k}t^{2k}}{(2k)!}}\!$

$={\frac {(-1)^{0}t^{2(0)}}{(2(0))!}}+{\frac {(-1)^{1}t^{2(1)}}{(2(1))!}}+{\frac {(-1)^{2}t^{2(2)}}{(2(2))!}}+{\frac {(-1)^{3}t^{2(3)}}{(2(3))!}}+...{\frac {(-1)^{k}t^{2k}}{(2k)!}}\!$

                                      $\cos t=1-{\frac {t^{2}}{2}}+{\frac {t^{4}}{24}}+{\frac {t^{6}}{720}}...{\frac {(-1)t^{2k}}{(2k)!}}\!$

$\sin t=\sum _{k=0}^{\infty }{\frac {(-1)^{k}t^{2k+1}}{(2k+1)!}}\!$

$={\frac {(-1)^{0}t^{2(0)+1}}{(2(0)+1)!}}+{\frac {(-1)^{1}t^{2(1)+1}}{(2(1)+1)!}}+{\frac {(-1)^{2}t^{2(2)+1}}{(2(2)+1)!}}+{\frac {(-1)^{3}t^{2(3)+1}}{(2(3)+1)!}}+...{\frac {(-1)^{k}t^{2k+1}}{(2k+1)!}}\!$

                                      $\sin t=t-{\frac {t^{3}}{6}}+{\frac {t^{5}}{120}}-{\frac {t^{7}}{5040}}+...{\frac {(-1)^{k}t^{2k+1}}{(2k+1)!}}\!$

--Egm4313.s12.team11.arrieta 17:07, 6 February 2012 (UTC)

Problem R2.8

Problem Statement

Find a general solution. Check your answer by substitution.

Problem 8

$y''+y'+3.25y=0\!$

Let:
$\lambda =d/dx\!$

Characteristic Equation

$\lambda ^{2}+\lambda +3.25=0\!$
Using the quadratic equation to find roots we get:
$\lambda _{1}={\frac {-1+i{\sqrt {(}}12)}{2}}\!$
$\lambda _{2}={\frac {-1-i{\sqrt {(}}12)}{2}}\!$
Therefore:

$y_{h}(x)=e^{-{\frac {1}{2}}x}(c_{1}\cos(x{\sqrt {3}})+c_{2}\sin(x{\sqrt {3}}))\!$

Check By Substitution

$y'(x)=-{\frac {1}{2}}e^{-{\frac {1}{2}}x}(c_{1}\cos(x{\sqrt {3}})+c_{2}\sin(x{\sqrt {3}})+e^{-{\frac {1}{2}}x}(-{\sqrt {3}}c_{1}\sin {{\sqrt {3}}x}+{\sqrt {3}}c_{1}\cos {{\sqrt {3}}x})\!$
$y''(x)={\frac {1}{4}}e^{-{\frac {1}{2}}x}(c_{1}\cos(x{\sqrt {3}})+c_{2}\sin(x{\sqrt {3}})-{\frac {1}{2}}e^{-{\frac {1}{2}}x}(-{\sqrt {3}}c_{1}\sin {{\sqrt {3}}x}+{\sqrt {3}}c_{1}\cos {{\sqrt {3}}x})-\!$
${\frac {1}{2}}e^{-{\frac {1}{2}}x}(-{\sqrt {3}}c_{1}\sin {{\sqrt {3}}x}+{\sqrt {3}}c_{1}\cos {{\sqrt {3}}x})e^{-{\frac {1}{2}}x}(-3c_{1}\cos(x{\sqrt {3}})-3c_{2}\sin(x{\sqrt {3}})\!$
Substituting $y,y',y''\!$ into the original equation, the result is

 $y''+y'+3.25y=0\!$

Problem 15

$y''+0.54y'+(0.0729+\pi )y=0\!$
Let: ${\frac {d}{dx}}=\lambda \!$

Characteristic Equation

$\lambda ^{2}+0.54\lambda +(0.0729+\pi )=0\!$
Using the quadratic equation to find roots we get:
$\lambda _{1}={\frac {-0.27+i{\sqrt {(}}\pi )}{2}}\!$
$\lambda _{2}={\frac {-0.27-i{\sqrt {(}}\pi )}{2}}\!$
Therefore:

$y_{h}(x)=e^{-0.27x}(c_{1}\cos(x{\sqrt {\pi }})+c_{2}\sin(x{\sqrt {\pi }})\!$

Check By Substitution

$y'(x)=-0.27e^{-0.27x}(c_{1}\cos(x{\sqrt {\pi }})+c_{2}\sin(x{\sqrt {\pi }})+e^{-0.27x}(-{\sqrt {\pi }}c_{1}\sin {{\sqrt {\pi }}x}+{\sqrt {\pi }}c_{1}\cos {{\sqrt {\pi }}x})\!$

$y''(x)=0.0729e^{-0.27x}(c_{1}\cos(x{\sqrt {\pi }})+c_{2}\sin(x{\sqrt {\pi }})-0.27e^{-0.27x}(-{\sqrt {\pi }}c_{1}\sin {{\sqrt {\pi }}x}+{\sqrt {\pi }}c_{1}\cos {{\sqrt {\pi }}x})-\!$

$0.27e^{-0.27x}({\sqrt {\pi }}c_{1}\sin {{\sqrt {\pi }}x}+{\sqrt {\pi }}c_{1}\cos {{\sqrt {\pi }}x})+e^{-0.27x}(-\pi (c_{1}\cos(x{\sqrt {\pi }}))-\pi (c_{2}\sin(x{\sqrt {\pi }})))\!$

Substituting $y,y',y''\!$ into the original equation, the result is

 $y''+0.54y'+(0.0729+\pi )y=0\!$

Egm4313.s12.team11.gooding 03:41, 7 February 2012 (UTC)

Report 2, Problem 9

Problem Statement

Find and plot the solution for the L2-ODE-CC corresponding to

$\lambda ^{2}+4\lambda +13\!$

with $r(x)=0\!$

and initial conditions $y(0)=1\!$, $y'(0)=0\!$

In another figure, superimpose 3 figs.:(a)this fig. (b) the fig. in R2.6 p.5-6, and (c) the fig. in R2.1 p.3-7

Quadratic Equation

$\lambda ={\frac {-b\pm {\sqrt {(}}b^{2}-4ac)}{2a}}\!$ with $a=1,b=4,c=13\!$

$\lambda ={\frac {-4\pm {\sqrt {(}}4^{2}-4*1*13)}{2*1}}=-2\pm 3i\!$

$\lambda =-2\pm 3i\!$

Homogeneous Solution

The solution to a L2-ODE-CC with two complex roots is given by

$y(x)=e^{-{\frac {a}{2}}x}[Acos(\omega x)+Bsin(\omega x)]\!$

where $\lambda =-{\frac {a}{2}}\pm \omega i=-2\pm 3i\!$

$y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]\!$

Solving for A and B

first initial condition $y(0)=1\!$

$y(x)=e^{-2x}[Acos(3x)+Bsin(3x)]\!$

$y(0)=e^{-2*0}[Acos(3*0)+Bsin(3*0)]=1\!$

$A=1\!$

second initial condition $y'(0)=0\!$

$y'(x)={\frac {d}{dx}}y(x)={\frac {d}{dx}}e^{-2x}[cos(3x)+Bsin(3x)]\!$

$y'(x)=e^{-2x}[(-2B-3)sin(3x)+(3B-2)cos(3x)]\!$

$y'(0)=e^{-2*0}[(-2B-3)sin(3*0)+(3B-2)cos(3*0)]\!$

$0=3B-2\!$

$B={\frac {2}{3}}\!$

so the solution to our L2-ODE-CC is

                      $y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)]\!$

Solution to R2.6

After solving for the constants ${\frac {k}{c}}$ and ${\frac {k}{m}}$ we have the following homogeneous equation

$y''(x)+6y'(x)+9y=0\!$

Characteristic Equation and Roots

$\lambda ^{2}+6\lambda +9=0\!$

$(\lambda +3)(\lambda +3)=0\!$

We have a real double root $\lambda =-3\!$

Homogeneous Solution

We know the homogeneous solution to a L2-ODE-CC with a double real root to be

$y(x)=c_{1}e^{\lambda x}+c_{2}xe^{\lambda x}\!$

Assuming object starts from rest

$y(0)=1\!$, $y'(0)=0\!$

Plugging in $\lambda$ and applying our first initial condition

$y(0)=c_{1}e^{-3*0}+c_{2}*0*e^{-3*0}=1\!$

$c_{1}=1\!$

Taking the derivative and applying our second condition

$y'(x)={\frac {d}{dx}}y(x)={\frac {d}{dx}}e^{-3x}+c_{2}xe^{-3x}\!$

$y'(x)=-3e^{-3x}+c_{2}e^{-3x}-3c_{2}xe^{-3x}\!$

$y'(0)=-3e^{-3*0}+c_{2}e^{-3*0}-3c_{2}*0*e^{-3*0}=0\!$

$c_{2}=3\!$

Giving us the final solution

                 $y(x)=e^{-3x}+3xe^{-3x}\!$

Plots

Solution to this Equation

$y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)]\!$

Superimposed Graph

Our solution: $y(x)=e^{-2x}[cos(3x)+{\frac {2}{3}}sin(3x)]\!$ shown in blue

Equation for fig. in R2.1 p.3-7: $y(x)={\frac {5}{4}}e^{-2x}-{\frac {1}{4}}e^{5x}\!$ shown in red

Equation for fig. in R2.6 p.5-6:$y(x)=e^{-3x}+3xe^{-3x}\!$ shown in green