Fast Fourier transform

Subject classification: this is a mathematics resource.

This page is still under construction. Any contribution is appreciated.

Fast Fourier Transform

Fast fourier transform or FFT is an algorithm mainly developed for digital computing of a Discrete Fourier transform or DFT of a discrete signal. Computing of DFT of a digital signal (discrete-time signal) involves N² Complex multiplications , where N is the number of points to which we consider taking DFT of the input periodic signal . Using an FFT algorithm, the number of complex multiplications can be reduced to a greater extent. Reduction is mainly due to decimation either in time domain or in frequency domain

Decimation in time FFT algorithm (Radix 2)

The N-point DFT of a sequence is given by

$DFT\{x(n)\}=\sum _{n=0}^{N-1}x(n)w_{N}^{kn}{\text{ ; }}k=0,1,\cdots N-1.$

every time x(n) gets multiplied by $w_{N}^{kn}$ , we get one complex multiplication. Therefore when the above summation is expanded for a given $k$ , we get $N$ complex multiplications. Which means that, to compute Npoint DFT, we have $N\times N=N^{2}$ complex multiplications.
Our aim is to reduce the number of complex multiplications. In the following presentation, The number of samples of $x(n)$ is assumed to be a power of 2. i.e, $N=2^{v}$ where v is some fixed positive integer.
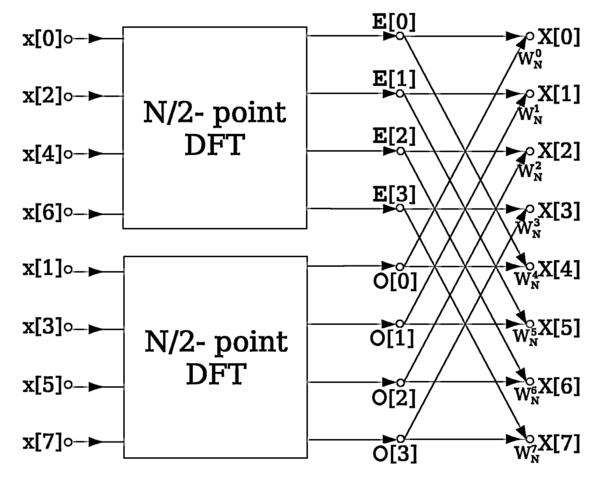
In this approach, N point transforms are broken into ${\frac {N}{2}}$ point DFTs which are further broken into ${\frac {N}{4}}$ point DFTs. And this process is continued until we get 2-point DFT. This technique is known as Divide and Conquer approach.


Let $x(n)$ be a finite length sequence of length equal to N. Given sequence is : $x(n)=x(1),x(2),x(3),\cdots x(N-2),x(N-1).$
Even indexed sequence is : $x_{e}(n)=x(0),x(2),x(4)\cdots x(N-2).$
and, odd indexed sequence is : $x_{o}(n)=x(1),x(3),x(5)\cdots x(N-1).$

Now we can split the above DFT equation into even and odd parts as below :

$X(k)=\underbrace {\sum _{n=0}^{N-2}x(n)w_{N}^{kn}} ^{\text{Even indexed}}+\underbrace {\sum _{n=0}^{N-1}x(n)w_{N}^{kn}} ^{\text{Odd indexed}}$

Letting $N=2r$ in the first summation and $N=2r+1$ in the second summation, we get :

$X(k)=\sum _{r=0}^{{\frac {N}{2}}-1}x(2r)w_{N}^{2kr}+\sum _{r=0}^{{\frac {N}{2}}-1}x(2r+1)w_{N}^{k(2r+1)}$

since,

$w_{N}^{k2r)}=e^{-j{\frac {2\pi }{N}}k2r}=e^{-j{\frac {2\pi }{\left({\frac {N}{2}}\right)}}kr}=w_{\left({\frac {N}{2}}\right)}^{kr}$

We get

$X(k)=\sum _{r=0}^{{\frac {N}{2}}-1}x(2r)w_{\left({\frac {N}{2}}\right)}^{kr}+w_{N)}^{k}\sum _{r=0}^{{\frac {N}{2}}-1}x(2r+1)w_{\left({\frac {N}{2}}\right)}^{kr}$

$\implies X(k)=G(k)+w_{N}^{k}H(k){\text{ ; }}k=0,1,2\cdots {\frac {N}{2}}-1{\text{ or just }}0\leq k\leq {\frac {N}{2}}-1$

Where $G(k)$ and $H(k)$ are ${\frac {N}{2}}$ point DFTs of even indexed and odd indexed sequences, respectively. For computing $X(k)$ for ${\frac {N}{2}}\leq k\leq N-1$ , the periodicity of $G(k)$ and $H(k)$ are exploited. Since $G(k)$ and $H(k)$ are ${\frac {N}{2}}$-point DFTs, they are implicit periodic with a fundamental period ${\frac {N}{2}}$ . Hence, we may write

$X(k)=G(k)+w_{N}^{k}H(k){\text{ when }}0\leq k\leq {\frac {N}{2}}-1{\text{ and }}$

$X(k)=G(k+{\frac {N}{2}})+w_{N}^{k}H(k+{\frac {N}{2}}){\text{ when }}{\frac {N}{2}}-1\leq k\leq N-1$

Now, after first decimation, the total number of complex multiplications is, $\eta _{1}=2\left({\frac {N}{2}}^{2}\right)+N$

The same way will lead us to further decimation and thus a block diagram can be contructed as below :

Prepared from the notes of Dr. D. Ganesh Rao Tutorials, Bangalore

The derivation or the text in this article written by Sushruth Sastry 22:13, 19 November 2010 (UTC) is the content from the Tution notes of Dr. D. Ganesh rao, Prof. at MSRIT, bangalore.