Elastic plate with circular hole under shear
Given:
Large plate in pure shear.
Stress state perturbed by a small hole. The BCs are
at
r
=
a
{\displaystyle r=a}
(103)
t
r
=
t
θ
=
0
;
n
^
=
−
e
^
r
⇒
σ
r
r
=
σ
r
θ
=
0
{\displaystyle {\text{(103)}}\qquad t_{r}=t_{\theta }=0~;~~{\widehat {\mathbf {n} }}=-{\widehat {\mathbf {e} }}~r\Rightarrow \sigma _{rr}=\sigma _{r\theta }=0}
at
r
→
∞
{\displaystyle r\rightarrow \infty }
(104)
σ
12
→
S
;
σ
11
→
0
;
σ
22
→
0
{\displaystyle {\text{(104)}}\qquad \sigma _{12}\rightarrow S~;~~\sigma _{11}\rightarrow 0~;~~\sigma _{22}\rightarrow 0}
We will solve this problem by superposing a perturbation due to the hole on the unperturbed solution. The effect of the perturbation will decrease with increasing distance from the hole, i.e. the effect will be proportional to
r
−
n
{\displaystyle r^{-n}\,}
(105)
σ
11
=
σ
22
=
0
;
σ
12
=
S
{\displaystyle {\text{(105)}}\qquad \sigma _{11}=\sigma _{22}=0~;~~\sigma _{12}=S}
Therefore,
(106)
σ
12
=
−
φ
,
12
=
S
{\displaystyle {\text{(106)}}\qquad \sigma _{12}=-\varphi _{,12}=S}
Integrating,
(107)
φ
,
1
=
−
S
x
2
+
f
(
x
1
)
⇒
φ
=
−
S
x
1
x
2
+
∫
f
(
x
1
)
d
x
1
{\displaystyle {\text{(107)}}\qquad \varphi _{,1}=-Sx_{2}+f(x_{1})\Rightarrow \varphi =-Sx_{1}x_{2}+\int f(x_{1})dx_{1}}
Since
φ
{\displaystyle \varphi }
(108)
φ
=
−
S
x
1
x
2
=
−
S
(
r
cos
θ
)
(
r
sin
θ
)
=
−
S
r
2
2
sin
(
2
θ
)
{\displaystyle {\text{(108)}}\qquad \varphi =-Sx_{1}x_{2}=-S(r\cos \theta )(r\sin \theta )=-{\cfrac {Sr^{2}}{2}}\sin(2\theta )}
or,
(109)
φ
=
−
S
r
2
2
sin
(
2
θ
)
{\displaystyle {\text{(109)}}\qquad \varphi =-{\cfrac {Sr^{2}}{2}}\sin(2\theta )}
Note that we have arranged the expression so that it has a form similar to the Fourier series of the previous section.
For this we have to add terms to
φ
{\displaystyle \varphi }
The unperturbed solution continues to be true as
r
→
∞
{\displaystyle r\rightarrow \infty \,}
The terms have the same form as the unperturbed solution,i.e.,
s
i
n
(
2
θ
)
{\displaystyle sin(2\theta )\,}
The new
φ
{\displaystyle \varphi }
r
−
n
{\displaystyle r^{-n}\,}
Recall,
φ
=
∑
n
=
0
∞
f
n
(
r
)
cos
(
n
θ
)
+
∑
n
=
0
∞
g
n
(
r
)
sin
(
n
θ
)
{\displaystyle \varphi =\sum _{n=0}^{\infty }f_{n}(r)\cos(n\theta )+\sum _{n=0}^{\infty }g_{n}(r)\sin(n\theta )}
where,
f
0
(
r
)
=
A
0
r
2
+
B
0
r
2
ln
r
+
C
0
+
D
0
ln
r
f
1
(
r
)
=
A
1
r
3
+
B
1
r
+
C
1
r
ln
r
+
D
1
r
−
1
f
n
(
r
)
=
A
n
r
n
+
2
+
B
n
r
n
+
C
n
r
−
n
+
2
+
D
n
r
−
n
,
n
>
1
{\displaystyle {\begin{aligned}f_{0}(r)&=A_{0}r^{2}+B_{0}r^{2}\ln r+C_{0}+D_{0}\ln r\\f_{1}(r)&=A_{1}r^{3}+B_{1}r+C_{1}r\ln r+D_{1}r^{-1}\\f_{n}(r)&=A_{n}r^{n+2}+B_{n}r^{n}+C_{n}r^{-n+2}+D_{n}r^{-n}~,~~n>1\end{aligned}}}
So the appropriate stress function for the perturbation is
(110)
φ
=
g
2
(
r
)
sin
(
2
θ
)
=
(
C
2
r
−
2
+
2
+
D
2
r
−
2
)
sin
(
2
θ
)
{\displaystyle {\text{(110)}}\qquad \varphi =g_{2}(r)\sin(2\theta )=\left(C_{2}r^{-2+2}+D_{2}r^{-2}\right)\sin(2\theta )}
or,
(111)
φ
=
(
C
2
+
D
2
r
−
2
)
sin
(
2
θ
)
{\displaystyle {\text{(111)}}\qquad \varphi =\left(C_{2}+D_{2}r^{-2}\right)\sin(2\theta )}
Hence, the stress function appropriate for the superposed solution is
(112)
φ
=
−
S
r
2
2
sin
(
2
θ
)
+
(
C
2
+
D
2
r
−
2
)
sin
(
2
θ
)
{\displaystyle {\text{(112)}}\varphi =-{\cfrac {Sr^{2}}{2}}\sin(2\theta )+\left(C_{2}+D_{2}r^{-2}\right)\sin(2\theta )}
We determine
C
2
{\displaystyle C_{2}}
D
2
{\displaystyle D_{2}}
r
=
a
{\displaystyle r=a}
The stresses are
(113)
σ
r
r
=
1
r
∂
φ
∂
r
+
1
r
2
∂
2
φ
∂
θ
2
=
(
S
−
4
C
2
r
−
2
−
6
D
2
r
−
4
)
sin
(
2
θ
)
(114)
σ
θ
θ
=
∂
2
φ
∂
r
2
=
(
−
S
+
6
D
2
r
−
4
)
sin
(
2
θ
)
(115)
σ
r
θ
=
−
∂
∂
r
(
1
r
∂
φ
∂
θ
)
=
(
S
+
6
D
2
r
−
4
)
cos
(
2
θ
)
{\displaystyle {\begin{aligned}{\text{(113)}}\qquad \sigma _{rr}&={\cfrac {1}{r}}{\cfrac {\partial \varphi }{\partial r}}+{\cfrac {1}{r^{2}}}{\cfrac {\partial ^{2}\varphi }{\partial \theta ^{2}}}=\left(S-4C_{2}r^{-2}-6D_{2}r^{-4}\right)\sin(2\theta )\\{\text{(114)}}\qquad \sigma _{\theta \theta }&={\cfrac {\partial ^{2}\varphi }{\partial r^{2}}}=\left(-S+6D_{2}r^{-4}\right)\sin(2\theta )\\{\text{(115)}}\qquad \sigma _{r\theta }&=-{\cfrac {\partial }{\partial r}}\left({\cfrac {1}{r}}{\cfrac {\partial \varphi }{\partial \theta }}\right)=\left(S+6D_{2}r^{-4}\right)\cos(2\theta )\end{aligned}}}
Hence,
(116)
σ
r
r
|
r
=
a
=
0
=
(
S
−
4
C
2
a
−
2
−
6
D
2
a
−
4
)
sin
(
2
θ
)
(117)
σ
r
θ
|
r
=
a
=
0
=
(
S
+
2
C
2
a
−
2
+
6
D
2
a
−
4
)
cos
(
2
θ
)
{\displaystyle {\begin{aligned}{\text{(116)}}\qquad \left.\sigma _{rr}\right|_{r=a}&=0=\left(S-4C_{2}a^{-2}-6D_{2}a^{-4}\right)\sin(2\theta )\\{\text{(117)}}\qquad \left.\sigma _{r\theta }\right|_{r=a}&=0=\left(S+2C_{2}a^{-2}+6D_{2}a^{-4}\right)\cos(2\theta )\end{aligned}}}
or,
(118)
4
C
2
a
−
2
+
6
D
2
a
−
4
=
S
(119)
2
C
2
a
−
2
+
6
D
2
a
−
4
=
−
S
{\displaystyle {\begin{aligned}{\text{(118)}}\qquad 4C_{2}a^{-2}+6D_{2}a^{-4}&=S\\{\text{(119)}}\qquad 2C_{2}a^{-2}+6D_{2}a^{-4}&=-S\end{aligned}}}
Solving,
(120)
C
2
=
S
a
2
;
D
2
=
−
S
a
4
2
{\displaystyle {\text{(120)}}\qquad C_{2}=Sa^{2}~;~~D_{2}=-{\cfrac {Sa^{4}}{2}}}
Back substituting,
(121)
σ
r
r
=
S
(
1
−
4
a
2
r
2
+
3
a
4
r
4
)
sin
(
2
θ
)
(122)
σ
θ
θ
=
S
(
−
1
−
3
a
4
r
4
)
sin
(
2
θ
)
(123)
σ
r
θ
=
S
(
1
+
2
a
2
r
2
−
3
a
4
r
4
)
cos
(
2
θ
)
{\displaystyle {\begin{aligned}{\text{(121)}}\qquad \sigma _{rr}&=S\left(1-4{\cfrac {a^{2}}{r^{2}}}+3{\cfrac {a^{4}}{r^{4}}}\right)\sin(2\theta )\\{\text{(122)}}\qquad \sigma _{\theta \theta }&=S\left(-1-3{\cfrac {a^{4}}{r^{4}}}\right)\sin(2\theta )\\{\text{(123)}}\qquad \sigma _{r\theta }&=S\left(1+2{\cfrac {a^{2}}{r^{2}}}-3{\cfrac {a^{4}}{r^{4}}}\right)\cos(2\theta )\end{aligned}}}
Consider the elastic plate with a hole subject to pure shear.
Elastic plate with a circular hole under pure shear
The stresses close to the hole are given by
(29)
σ
r
r
=
S
(
1
−
4
a
2
r
2
+
3
a
4
r
4
)
sin
(
2
θ
)
(30)
σ
θ
θ
=
S
(
−
1
−
3
a
4
r
4
)
sin
(
2
θ
)
(31)
σ
r
θ
=
S
(
1
+
2
a
2
r
2
−
3
a
4
r
4
)
cos
(
2
θ
)
{\displaystyle {\begin{aligned}{\text{(29)}}\qquad \sigma _{rr}&=S\left(1-4{\frac {a^{2}}{r^{2}}}+3{\frac {a^{4}}{r^{4}}}\right)\sin(2\theta )\\{\text{(30)}}\qquad \sigma _{\theta \theta }&=S\left(-1-3{\frac {a^{4}}{r^{4}}}\right)\sin(2\theta )\\{\text{(31)}}\qquad \sigma _{r\theta }&=S\left(1+2{\frac {a^{2}}{r^{2}}}-3{\frac {a^{4}}{r^{4}}}\right)\cos(2\theta )\end{aligned}}}
Show that the normal and shear traction boundary conditions far from the hole are satisfied by these stresses.
Calculate the stress concentration factors at the hole, i.e., (
τ
max
/
S
{\displaystyle \tau _{\text{max}}/S}
σ
max
/
σ
0
{\displaystyle \sigma _{\text{max}}/\sigma _{0}}
Calculate the displacement field corresponding to this stress field (for plane stress). Plot the deformed shape of the hole.
Far from the hole,
r
=
∞
{\displaystyle r=\infty }
(32)
σ
r
r
=
S
sin
(
2
θ
)
(33)
σ
θ
θ
=
−
S
sin
(
2
θ
)
(34)
σ
r
θ
=
S
cos
(
2
θ
)
{\displaystyle {\begin{aligned}{\text{(32)}}\qquad \sigma _{rr}&=S\sin(2\theta )\\{\text{(33)}}\qquad \sigma _{\theta \theta }&=-S\sin(2\theta )\\{\text{(34)}}\qquad \sigma _{r\theta }&=S\cos(2\theta )\end{aligned}}}
To rotate the stresses back to the
(
x
1
,
x
2
)
{\displaystyle (x_{1},x_{2})}
(35)
[
σ
11
σ
12
σ
13
σ
21
σ
22
σ
23
σ
31
σ
32
σ
33
]
=
[
cos
θ
−
sin
θ
0
sin
θ
cos
θ
0
0
0
1
]
[
σ
r
r
σ
r
θ
σ
r
z
σ
r
θ
σ
θ
θ
σ
θ
z
σ
r
z
σ
θ
z
σ
z
z
]
[
cos
θ
sin
θ
0
−
sin
θ
cos
θ
0
0
0
1
]
{\displaystyle {\text{(35)}}\qquad {\begin{bmatrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{bmatrix}}={\begin{bmatrix}\cos \theta &-\sin \theta &0\\\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\sigma _{rr}&\sigma _{r\theta }&\sigma _{rz}\\\sigma _{r\theta }&\sigma _{\theta \theta }&\sigma _{\theta z}\\\sigma _{rz}&\sigma _{\theta z}&\sigma _{zz}\end{bmatrix}}{\begin{bmatrix}\cos \theta &\sin \theta &0\\-\sin \theta &\cos \theta &0\\0&0&1\end{bmatrix}}}
Setting
σ
r
z
=
0
{\displaystyle \sigma _{rz}=0}
σ
θ
z
=
0
{\displaystyle \sigma _{\theta z}=0}
(36)
σ
11
=
σ
r
r
cos
2
θ
+
σ
θ
θ
sin
2
θ
−
σ
r
θ
sin
(
2
θ
)
(37)
σ
22
=
σ
r
r
sin
2
θ
+
σ
θ
θ
cos
2
θ
+
σ
r
θ
sin
(
2
θ
)
(38)
σ
12
=
σ
r
r
−
σ
θ
θ
2
sin
(
2
θ
)
+
σ
r
θ
cos
(
2
θ
)
{\displaystyle {\begin{aligned}{\text{(36)}}\qquad \sigma _{11}&=\sigma _{rr}\cos ^{2}\theta +\sigma _{\theta \theta }\sin ^{2}\theta -\sigma _{r\theta }\sin(2\theta )\\{\text{(37)}}\qquad \sigma _{22}&=\sigma _{rr}\sin ^{2}\theta +\sigma _{\theta \theta }\cos ^{2}\theta +\sigma _{r\theta }\sin(2\theta )\\{\text{(38)}}\qquad \sigma _{12}&={\frac {\sigma _{rr}-\sigma _{\theta \theta }}{2}}\sin(2\theta )+\sigma _{r\theta }\cos(2\theta )\end{aligned}}}
Plugging in equations (32-34) in the above, we have
(39)
σ
11
=
−
S
[
sin
(
2
θ
)
cos
(
2
θ
)
−
sin
(
2
θ
)
cos
(
2
θ
)
]
=
0
(40)
σ
22
=
S
[
sin
(
2
θ
)
cos
(
2
θ
)
−
sin
(
2
θ
)
cos
(
2
θ
)
]
=
0
(41)
σ
12
=
S
[
sin
(
2
θ
)
sin
(
2
θ
)
+
cos
(
2
θ
)
cos
(
2
θ
)
]
=
S
{\displaystyle {\begin{aligned}{\text{(39)}}\qquad \sigma _{11}&=-S\left[\sin(2\theta )\cos(2\theta )-\sin(2\theta )\cos(2\theta )\right]=0\\{\text{(40)}}\qquad \sigma _{22}&=S\left[\sin(2\theta )\cos(2\theta )-\sin(2\theta )\cos(2\theta )\right]=0\\{\text{(41)}}\qquad \sigma _{12}&=S\left[\sin(2\theta )\sin(2\theta )+\cos(2\theta )\cos(2\theta )\right]=S\end{aligned}}}
Hence, the far field stress BCs are satisfied.
r
=
a
{\displaystyle r=a}
(42)
σ
r
r
=
S
(
1
−
4
+
3
)
sin
(
2
θ
)
=
0
(43)
σ
θ
θ
=
S
(
−
1
−
3
)
sin
(
2
θ
)
=
−
4
S
sin
(
2
θ
)
(44)
σ
r
θ
=
S
(
1
+
2
−
3
)
cos
(
2
θ
)
=
0
{\displaystyle {\begin{aligned}{\text{(42)}}\qquad \sigma _{rr}&=S\left(1-4+3\right)\sin(2\theta )=0\\{\text{(43)}}\qquad \sigma _{\theta \theta }&=S\left(-1-3\right)\sin(2\theta )=-4S\sin(2\theta )\\{\text{(44)}}\qquad \sigma _{r\theta }&=S\left(1+2-3\right)\cos(2\theta )=0\end{aligned}}}
The maximum (or minimum) hoop stress at the hole is at the locations
where
d
σ
θ
θ
/
d
θ
=
−
8
S
cos
(
2
θ
)
=
0
{\displaystyle d\sigma _{\theta \theta }/d\theta =-8S\cos(2\theta )=0}
θ
=
π
/
4
{\displaystyle \theta =\pi /4}
θ
=
3
π
/
4
{\displaystyle \theta =3\pi /4}
(45)
at
θ
=
π
4
σ
θ
θ
=
−
4
S
(46)
at
θ
=
3
π
4
σ
θ
θ
=
4
S
{\displaystyle {\begin{aligned}{\text{(45)}}\qquad {\text{at}}~\theta ={\frac {\pi }{4}}&&\sigma _{\theta \theta }=-4S\\{\text{(46)}}\qquad {\text{at}}~\theta ={\frac {3\pi }{4}}&&\sigma _{\theta \theta }=4S\end{aligned}}}
The maximum shear stress is given by
(47)
τ
max
=
1
2
|
σ
r
r
−
σ
θ
θ
|
=
2
S
{\displaystyle {\text{(47)}}\qquad \tau _{\text{max}}={\frac {1}{2}}\left|\sigma _{rr}-\sigma _{\theta \theta }\right|=2S}
Therefore, the stress concentration factors are
(48)
σ
max
S
=
4
;
τ
max
S
=
2
{\displaystyle {\text{(48)}}\qquad {\frac {\sigma _{\text{max}}}{S}}=4~;~~{\frac {\tau _{\text{max}}}{S}}=2}
The stress function used to derive the above results was
(49)
φ
=
−
S
2
r
2
sin
(
2
θ
)
+
S
a
2
sin
(
2
θ
)
−
S
a
4
2
r
−
2
sin
(
2
θ
)
{\displaystyle {\text{(49)}}\qquad \varphi =-{\frac {S}{2}}r^{2}\sin(2\theta )+Sa^{2}\sin(2\theta )-{\frac {Sa^{4}}{2}}r^{-2}\sin(2\theta )}
From Michell's solution , the displacements corresponding
to the above stress function are given by
(50)
2
μ
u
r
=
−
S
2
[
−
2
r
sin
(
2
θ
)
]
+
S
a
2
[
(
κ
+
1
)
r
−
1
sin
(
2
θ
)
]
−
S
a
4
2
[
2
r
−
3
sin
(
2
θ
)
]
(51)
2
μ
u
θ
=
−
S
2
[
−
2
r
cos
(
2
θ
)
]
+
S
a
2
[
(
κ
−
1
)
r
−
1
cos
(
2
θ
)
]
−
S
a
4
2
[
−
2
r
−
3
cos
(
2
θ
)
]
{\displaystyle {\begin{aligned}{\text{(50)}}\qquad 2\mu u_{r}&=-{\frac {S}{2}}\left[-2r\sin(2\theta )\right]+Sa^{2}\left[(\kappa +1)r^{-1}\sin(2\theta )\right]-{\frac {Sa^{4}}{2}}\left[2r^{-3}\sin(2\theta )\right]\\{\text{(51)}}\qquad 2\mu u_{\theta }&=-{\frac {S}{2}}\left[-2r\cos(2\theta )\right]+Sa^{2}\left[(\kappa -1)r^{-1}\cos(2\theta )\right]-{\frac {Sa^{4}}{2}}\left[-2r^{-3}\cos(2\theta )\right]\end{aligned}}}
or,
(52)
u
r
=
S
r
sin
(
2
θ
)
2
μ
[
1
+
(
κ
+
1
)
a
2
r
2
−
a
4
r
4
]
(53)
u
θ
=
S
r
cos
(
2
θ
)
2
μ
[
1
+
(
κ
−
1
)
a
2
r
2
+
a
4
r
4
]
{\displaystyle {\begin{aligned}{\text{(52)}}\qquad u_{r}&={\frac {Sr\sin(2\theta )}{2\mu }}\left[1+(\kappa +1){\frac {a^{2}}{r^{2}}}-{\frac {a^{4}}{r^{4}}}\right]\\{\text{(53)}}\qquad u_{\theta }&={\frac {Sr\cos(2\theta )}{2\mu }}\left[1+(\kappa -1){\frac {a^{2}}{r^{2}}}+{\frac {a^{4}}{r^{4}}}\right]\end{aligned}}}
For plane stress,
κ
=
(
3
−
ν
)
/
(
1
+
ν
)
{\displaystyle \kappa =(3-\nu )/(1+\nu )}
(54)
u
r
=
S
r
sin
(
2
θ
)
2
μ
[
1
+
(
4
1
+
ν
)
a
2
r
2
−
a
4
r
4
]
(55)
u
θ
=
S
r
cos
(
2
θ
)
2
μ
[
1
+
2
(
1
−
ν
1
+
ν
)
a
2
r
2
+
a
4
r
4
]
{\displaystyle {\begin{aligned}{\text{(54)}}\qquad u_{r}&={\frac {Sr\sin(2\theta )}{2\mu }}\left[1+\left({\frac {4}{1+\nu }}\right){\frac {a^{2}}{r^{2}}}-{\frac {a^{4}}{r^{4}}}\right]\\{\text{(55)}}\qquad u_{\theta }&={\frac {Sr\cos(2\theta )}{2\mu }}\left[1+2\left({\frac {1-\nu }{1+\nu }}\right){\frac {a^{2}}{r^{2}}}+{\frac {a^{4}}{r^{4}}}\right]\end{aligned}}}
At
r
=
a
{\displaystyle r=a}
(56)
u
r
=
S
a
sin
(
2
θ
)
μ
(
2
1
+
ν
)
(57)
u
θ
=
S
a
cos
(
2
θ
)
μ
(
2
1
+
ν
)
{\displaystyle {\begin{aligned}{\text{(56)}}\qquad u_{r}&={\frac {Sa\sin(2\theta )}{\mu }}\left({\frac {2}{1+\nu }}\right)\\{\text{(57)}}\qquad u_{\theta }&={\frac {Sa\cos(2\theta )}{\mu }}\left({\frac {2}{1+\nu }}\right)\end{aligned}}}
Now
μ
=
E
/
2
(
1
+
ν
)
{\displaystyle \mu =E/2(1+\nu )}
(58)
u
r
=
4
S
a
sin
(
2
θ
)
E
(59)
u
θ
=
4
S
a
cos
(
2
θ
)
E
{\displaystyle {\begin{aligned}{\text{(58)}}\qquad u_{r}&={\frac {4Sa\sin(2\theta )}{E}}\\{\text{(59)}}\qquad u_{\theta }&={\frac {4Sa\cos(2\theta )}{E}}\end{aligned}}}
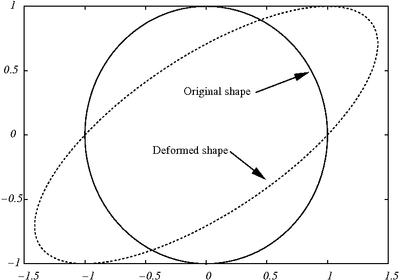
The deformed shape is shown below
Displacement field near a hole in plate under pure shear






































![{\displaystyle {\begin{aligned}{\text{(39)}}\qquad \sigma _{11}&=-S\left[\sin(2\theta )\cos(2\theta )-\sin(2\theta )\cos(2\theta )\right]=0\\{\text{(40)}}\qquad \sigma _{22}&=S\left[\sin(2\theta )\cos(2\theta )-\sin(2\theta )\cos(2\theta )\right]=0\\{\text{(41)}}\qquad \sigma _{12}&=S\left[\sin(2\theta )\sin(2\theta )+\cos(2\theta )\cos(2\theta )\right]=S\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62e8c34f2f2ae2dfc85d130284af3d5cf1d8a000)








![{\displaystyle {\begin{aligned}{\text{(50)}}\qquad 2\mu u_{r}&=-{\frac {S}{2}}\left[-2r\sin(2\theta )\right]+Sa^{2}\left[(\kappa +1)r^{-1}\sin(2\theta )\right]-{\frac {Sa^{4}}{2}}\left[2r^{-3}\sin(2\theta )\right]\\{\text{(51)}}\qquad 2\mu u_{\theta }&=-{\frac {S}{2}}\left[-2r\cos(2\theta )\right]+Sa^{2}\left[(\kappa -1)r^{-1}\cos(2\theta )\right]-{\frac {Sa^{4}}{2}}\left[-2r^{-3}\cos(2\theta )\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78bd8689956acb88a1cc4c0859e77ed7a49c9f59)
![{\displaystyle {\begin{aligned}{\text{(52)}}\qquad u_{r}&={\frac {Sr\sin(2\theta )}{2\mu }}\left[1+(\kappa +1){\frac {a^{2}}{r^{2}}}-{\frac {a^{4}}{r^{4}}}\right]\\{\text{(53)}}\qquad u_{\theta }&={\frac {Sr\cos(2\theta )}{2\mu }}\left[1+(\kappa -1){\frac {a^{2}}{r^{2}}}+{\frac {a^{4}}{r^{4}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7656b5cf9571fa0b62ca1dfd977270f3b852fff6)

![{\displaystyle {\begin{aligned}{\text{(54)}}\qquad u_{r}&={\frac {Sr\sin(2\theta )}{2\mu }}\left[1+\left({\frac {4}{1+\nu }}\right){\frac {a^{2}}{r^{2}}}-{\frac {a^{4}}{r^{4}}}\right]\\{\text{(55)}}\qquad u_{\theta }&={\frac {Sr\cos(2\theta )}{2\mu }}\left[1+2\left({\frac {1-\nu }{1+\nu }}\right){\frac {a^{2}}{r^{2}}}+{\frac {a^{4}}{r^{4}}}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce9c8f83816b2e58e1d51f8080ba30af484c4ffa)


