Economic Classroom Experiments/Private Value Auctions
| Economic Classroom Experiments/Private Value Auctions | |
|---|---|
| Designer | Originated by Todd Kaplan |
| Designed | 2007 |
| Topic | Auction |
| Archive of Simulations and Games for the Enhancement of the Learning Experience The individual resources in this archive come from diverse sources. They have been brought together into this archive in a project supported by | |
 | |
The Private Value Auction Experiment - Introduction
[edit | edit source]People sell and buy goods, equities, and financial assets through Auctions every day.
We explore the implications of the theory and experimental evidence for the first-price, and second-price auctions. We begin with a brief review of the experiment procedure, and proceed to the recent experimental results and compare them with the Nash equilibrium predictions. We then show how we can calculate the efficiency and try to measure the total surpluses.
Description of the Experiment
[edit | edit source]Software for running private-value auction experiments is available on Veconlab and econport. We used Veconlab in seven similar price auctions sessions, in each with different undergraduate and postgraduate students at the University of Exeter. After the participants were seated in a computer room, they began reading the instructions in the upper table. During the experiment we had two price auctions. In the first price auction all bidders bid and the highest bidder wins and pays his bid. We considered a game where each player receives a private value between $0 and $10 he would receive if he gets the good. No player knew the values of the others participants.
However, each bidder’s value for the underlying good is equally likely to be $0-$10 which is determined randomly. Every bidder knows his own value, and if both bids are the same it will be decided by the flip of a coin which bidder gets the good. The winner will have as return his own value minus his own bid. In other words, the buyer’s surplus is the difference between his certain value and his bid. If he does not win the auction, he has no return at all from the auction and will earn nothing from that round.
The number of students was 18 and for the whole experiment they are going to act as bidders. Each different form of auction was tested 7 rounds. In the First Price auction every bidder is being matched with a random bidder in each round and they bid for the same good. The highest bid receives the good. The same procedure is being following in the Second Price auction with the only difference that this time the highest bidder wins the good and pays the highest losing bid. This means that he pays less than he was bidding.
After these 2 sessions we repeat the experiment for the First Price auctions with higher amount of players. The only difference was the number of the bidders that were matched. We run 1 session of 7 rounds with 3 bidders matched, and then we run the same procedure with 4 bidders matched.
Recommended Testing
[edit | edit source]A simple (5-10 minute) test is essential to develop the confidence and experience needed for a smooth classroom implementation. To test this program, we should set up an experiment for only two participants (not necessary, but it speeds up the testing). Here are the instructions that are illustrated to the students before the experiment starts:
- Rounds: The experiment consists of a sequence of "rounds".
- Matching: In each round, you will be matched with a different person. Each of you will submit a bid for a prize being sold in an auction.
- Prize Values: Before bidding, you will be given a "prize value" which is the money value to you for the item being auctioned. Prize values, which will be determined randomly, will differ from person to person as explained below.
- Bid: After finding out your prize value, you begin by choosing a number or "bid". The other person will also choose a bid at the same time. You cannot see their prize value or their bid while making yours, and vice versa.
- Earnings: A bid is required to be a number, and the person with the high bid will purchase the item being sold. A random "coin flip" will select the winner in the event of a tie bid. The winner will earn their own prize value minus their own bid. The other bidder will earn nothing for that round.
Examples:
- If your prize value is 2 cents and you make a bid of 1 cent, then you would earn 2 - 1 = 1 cent if you have the high bid, and you would earn 0 otherwise.
- Suppose that both you and the other person tie with bids of 2 cents. Then we would use a computer-generated random number to select the winner, who would earn the difference between that person's prize value and the bid of 2 cents. The loser would earn 0 cents. The random tie-breaking device is like a fair coin flip, it ensures that each person has an equal chance of winning in the event of a tie, regardless of their value, their bid, or of whether or not they have won in previous rounds.
- The prize values will be determined randomly, so one person's value is likely to differ from that of another. Suppose a bidder with a value of 2 cents bids 1 and a bidder with a value of 3 cents bids 2, then the former would earn 0 and the latter would earn 3 - 2 = 1 cent.
- Note: The numbers used in the actual experiment to follow will be much larger than these numbers, which are for illustrative purposes only; the actual numbers are discussed next.
- Possible Values: At the beginning of each round, the computer will select a randomly determined value for you, which may be any penny amount between and including $0.00 and $10.00, with each amount in this interval being equally likely to be chosen. Imagine a roulette wheel with the stops labelled as 0.00, 0.01, ... 9.99, 10.00. Then a hard spin of the wheel would make each of these value amounts equally likely. Your value will be independent of any other person's value, so it is as if we spin the wheel once for you and a different time each other person. Your value in one period is independent of that in the next, so it is as if we spin the wheel for each bidder again at the start of each period.
- Bids: The round begins when you and the other person find out your own values, but neither of you will ever know the other's value. Then each of you will select a non-negative bid.
- You will be matched with the different persons in all rounds.
- There is a new random draw for each person at the start of a round to determine that person's value. Values are equally likely to be any penny amount between and including $0.00 and $10.00.
- After seeing their own value, each person will choose a bid that must be no greater than an upper limit: $10.00. The high bidder in each auction earns the difference between their value and their own bid, and the low bidder earns $0.00, with ties decided at random.
Theoretical background
[edit | edit source]Two of the basic ways of how Auctions can be theoretically modelled are private values or common values. In private value auctions bidders know their own value but are unaware about the value of the other participants. On the other hand in common value auctions, the object's value to each bidder is the same. In our experiment we are going to discuss about the private value auctions.
Some of the most common auction mechanisms are as follows:
The English Auction is where a single seller of a single item (or lot of items) receives increasing bids from prospective buyers. The auction ends by a predetermined stopping rule such as when a certain amount of time has passed before a new bid as been entered or at a predetermined time (such as with ebay) In this auction, the item goes to the highest bidder who pays his bid.
The Dutch auction has the seller start at the highest price and decrease price until someone is willing to buy the underlying good. The auction ends when either a buyer agrees to the price or the price reaches the minimum sale price. The buyer who first agrees gets the item for the current price. This has been used to sell flowers in both the Netherlands (hence, the name) and Japan. A varient of this mechanism is used on pricedrop.tv.
In the First Price Auction, bidders write sealed bids. The bidder with the highest bid wins and pays his bid. This is strategically equivalent to the Dutch Auction.
In the Second Price Auction the bidder with the highest bid wins the auction, but pays only the second highest bid (or the minimum bid/reserve price if none is given). This is also known as the Vickrey auction.
In an All Pay Auction everyone writes down a bid. The bidder with the highest bid wins the item; however, all bidders must pay their bids.
Equilibrium
[edit | edit source]The equilibrium concept used is one of Bayes-Nash, that is, an equilibrium is a bid as a function of value, where each bidder would not want to deviate from following this bid function given that other bidders are using it.
When bidders are risk neutral, the equilibrium in the first price auction is for all . (n = number of bidders). The equilibrium bid for a two bidder game will be ½ of the private value. Whilst it will be 2/3 for three bidders and ¾ for four bidders.
The equilibrium in the second-price auction is . The equilibrium in the all-pay auction is (if is uniformly distributed on ).
The equilibrium bid is in the following graphs always shown by the green vertical line. Theoretically, more bidders mean higher bids and thus more return for the seller. If all players would bid according to equilibrium, always the player with the highest private value won the auction. A state of efficiency.
Rules to auctions
[edit | edit source]In the experiment we deal with different forms of auctions. We have the First-Price Sealed-Bid Auction with two, three and four bidders and the Second-Price Sealed-Bid Auction and an All-Pay Auction as well.
The first form of Auction applied in the experiment is the simplest one, the first price auction where two bidders are competing with each other. All bidders know their own value for the good which is different from round to round. They wrote their bid in the Online form and the highest bidder wins the good and pays his bid. His personal return is the difference between the value and his bid. Each player has seven rounds playing with different bidders with this kind of auctions.
In the second part of the experiment a second price auction all bidders bid and the highest bidder wins the good and pays the highest losing bid. Also the competitor is chosen randomly and the bidders play seven rounds. Then we repeated two sessions of seven rounds by changing the number of the bidders who were matched in each round. This two sessions were only concerned the first price auctions.
Experimental economics’ Nash Equilibrium
[edit | edit source]Holt and Roth (2004, p4001) stated that:
‘Another emerging connection between game theory and experimentation is the increased use of the experimental methods in teaching. A well designed classroom experiment shows to students that the seemingly abstract equilibrium models can have surprising predictive power. The internet makes it easier to run complex games with large groups of students. For example, >30 different types of games, auctions and markets can be set up and run from site (http://veconlab.econ.virginia.edu/admin.htm). Most of the data displays and dynamically generated data graphs have options for hiding the relevant Nash predictions when the results are being discussed and then showing the Nash predictions subsequently’
Nash's most important contribution to game theory is the Nash equilibrium. He showed that in any competitive situation if the participants are rational, and they know that their opponents are rational, there can be only one optimal strategy.
All auctions have a Nash equilibrium, a bid that perfectly balances the risk of losing to a higher bidder (and making no profit) against the possibility of greater profits (the lower you bid, the more money you'll make).
Experimental procedure
[edit | edit source]- At the beginning of the experiment the participants were seated far away from each other and were given an introduction of the experiment. More specifically they were told the time that the experiment is going to last, during which they would be asked to take some decisions.
- Students have 5 minutes to read the instructions. After they had finished reading the instructions they have to answer two questions in order to show that they have totally understood the procedure.
- Instructor repeats the main information
- We have two session of which a number of subjects bids for a single unit of a commodity under a given pricing rule
- Every session is constitute by seven periods
- In each period every bidder is randomly being match with another bidder
- People make their decision and the sessions end
- Your bit determinates your round payoff as follows:
- If your bid is equal to the price, you will receive nothing
- The same procedure is being following to the second price auction with the only difference that this time the highest bidder wins the good and pays the highest losing bid.
- The earnings of the bidders are filled into an Excel Spreadsheet
- We compare our results with the predictions of Nash Equilibrium
Interpretation
[edit | edit source]In the beginning we must identify that the Nash equilibrium (A bid that perfectly balances the risk of losing to a higher bidder against the possibility of greater profits) is a very useful tool in order to make predictions. The predictions can be very accurate (accurate predictor) of how participants are going to behave during the experiment, but there is a strong possibility to have some divergences. When this happens automatically we are thinking of experiments where individuals act with different motivations.
To start with the analysis of the experimental data, we have to say that the results are very interesting because the participants did not have any experience in this kind of economic experiments. Thus the player will behave artless and will not try to follow any strategy they have heard of.
In the First Price and the Second Price auction we can observe that the results are above the predictions of the Nash equilibrium. In this particular experiment Nash equilibrium can be consider a persistently poor predictor. Participants seem not to conform to equilibrium behavior. Following the general theory, in both the First Price and the Second Price auction the object is sold to the bidder with the highest valuation of the good. However, you will see that the results of the experiment do not really support the theoretical results.
As we have identified before, in the first two auction sessions we have overbidding. This tendency of the participants to overbid can be explained in the following way. In both private values auctions the overbidding can be caused in terms of risk aversion. Risk aversion is the obvious suspect. Increasing risk aversion would make the bids increase overtime (from one auction to another- only when we have profit). In the Second Price auction some players obviously bid more than their private value because they expected the second bid to be lower then their private value. However, they risk having a negative payoff when the second bid is higher than their own valuation of the good. This behavior is likely because there are only two bidders competing against each other. This very risky behavior would probably disappear when more players are bidding in the auction. As Michael Abrams has mentioned ‘By the time an auctioneer shouts "Sold!" most bidders have already gone too far’.
Another reason why this may happen, is because is the first time the participants to experience and interact with this particular experiment. Further more the over bidding can be partial explained by this argument.
If we would repeat the experiment with the same participants many times we get probably results closer to Nash equilibrium predictions. Therefore learning can occur just by thinking about what the other participants will decide and the students will adjust their bids to that.
First Price Auction in Detail
[edit | edit source]Beneath you can see the result of the First Price auction in a diagram. There is a linear dependence between the private valuation of the good and the size of the corresponding bid. Following theory people would act rational by bidding the half of their private value which is shown by the green line i.e. you bid $3 when your private value is $6 and consequently your revenue would be $3 if you won the auction. People are trying to maximise their revenue because the revenue represents the utility from their purchase.
However a lot of participants bid more than the optimal bid and sometimes even their full private value which is shown by the red line. The overbidding may result from risk aversion as mentioned before or is maybe a consequence of the inexperience of the students. In general we can conclude that the participants of this experiment bid about 60% of their private value instead of the expected ration of 50%. Increasing the bid will increase the probability to win the auction but will decreases the surplus gained when winning. With bidding the private value the surplus will be zero.
| Average Private Value | Average Revenue | Average Winning Bid | Total Surplus | Efficiency |
| 5,27 | 1,57 | 5,16 | 6,73 | 0,968 |
The efficiency of the auction is nevertheless very high, about 97% of all auctions elected transferred the good to the player with the higher private value.
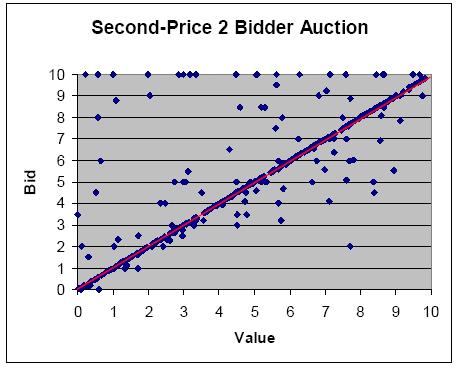
When we look at the Second Price auction we can see the tendency to bid the full private value was relatively high in this experiment. This is because participants know that their bid does not influence the price they have to pay. In the competition with one other student, most of the participants bid their private value aware that they only have to pay the lower bid. This would lead to efficiency because all goods would be transferred to the bidders with the higher valuation of the underlying object.
This, however, does not always hold because some people bid higher than their private value. This risky behavior must be seen as the attempt to certainly receive the good in combination with the hope that the other bid is low. The result was that some players had negative payoffs because the second bid was higher than their private value as well. So efficiency can be disturbed by such behavior. The overall efficiency was about 94% which means that in about 94% of the auctions the bidder with the higher valuation of the good has won the auction. This is a good value which indicates the efficiency of auctions. The average earnings have been about $2,6 per player and round. Obviously the average revenue for the player is higher in the Second Price than in the First Price auction. $2,6 > $1,56 is by nearly two third higher than in the other auction game.
| Average Private Value | Average Revenue | Average Winning Bid | Total Surplus | Efficiency |
| 4,86 | 2,61 | 3,53 | 6,14 | 0,944 |
A very likely explanation is that the winning bidders only have to pay the second highest bid which will automatically increase the revenue of the bidder. Even if the players bid more likely their private values than in the First Price experiment the revenues are going up. The average winning bid is much lower than in the other auction as well.
Distribution of the ‘pie'
[edit | edit source]The theory predicts that in the First Price auctions as in the Second Price auctions with two bidders the percentage of the bidders and sellers should be equally distributed. This means that 50% of the pie belongs to the bidder while the other half belongs to the seller.
For the First Price auctions with two bidders, the percentages of both the sellers and the buyers are not suiting theory. Moreover we have calculated that only 23% of the pie belongs to the bidder on average whilst 77% belongs to the sellers. The reason must be that the people can not use other bidders' prices as a guide, and as a result they tend to bid higher than they normally should. Also the participants are risk averse and are willing to have a lower expected revenue in order to higher probability to win the race. As a consequence the competition between the participants leads to overbidding and this behaviour is beneficial for the sellers.
In the Second Price auctions the percentages that we obtained are more closely to what the theory predicts. We have that 42% of the pie belongs to the bidder’s whist 58% belongs to the sellers.
Obviously the average revenue for the player is higher in the Second Price than in the First Price auction. A logical explanation is that the winning bidder only has to pay the second highest bid which will automatically increase the revenue of the bidder and decrease the revenue of the seller. Thus we have a result which is more similar to theory than the First Price auction. Joy of wining Cox, Smith, and Walker (1983b, 1988) and Goerre, Holt, and Palfrey (2000) suggested as an alternative explanation for overbidding in the first price auctions a model, where bidders receive a utility from the event of winning the auction. This pure joy of winning model with out risk aversion explains overbidding in single unit first price auctions. Increasing the number of the bidders (only for the first price auctions) In this part we are going to increase the number of the bidders ( 3 bidders and four bidders), in order to observe what is happening when we increase the number of the participants which act as bidders. The rounds that are described below in the figure 3 concerned only the first price auctions. Following the rule how to bid the optimal value which we have derived earlier, the optimal bid would be 2/3 of the private value.
Again we can see that there is a linear dependence between the private valuation of the good and the size of the corresponding bid. The green line again represents what the people would have bid if they act rational, by bidding the 2/3 of their private value.
We can observe that most of the participants overbid and sometimes their bids excided their private value. We can easily see that the results are similar to those of the First price auction with 2 bidders; again the overbidding dominates in the experiment.
The reasons for this overbidding is that in the First and the Second Price auctions people can not use other bidders' prices as a guide, and as a result they tend to bid higher than they normally would (than their private value). Also as we have mentioned before the risk aversion may a cause this overbidding.
The experiment continued by increasing the number of the bidders to 4. The green line represents what the participants would have bid if they act rational and the red line means bidding the full private value. We can observe that the results are almost the same in comparison to the previous examples. The most of the participants bid more then ¾ of their private value and many times they bid all of their private value. Thus overbidding continues. The reasons for the overbidding are the same as they have been describe above.
In both cases we have an increase at the number of the bidders to 3 and 4. The results remain the same as in the case with the First Price auctions with 2 bidders. We saw that the overbidding dominates in all of our cases. From this we can conclude that the number of the participants which act as bidders does not affect our results. With a larger number of bidders the overbidding goes on and the bids are becoming even higher than before. Because the players are risk averse and can not use other bidders' values as a guideline, and as a result they tend to bid higher than they normally would.
As previous research has shown, English auctions tend to create higher prices for the seller because of the way it is organized. The participants observe the other bids and can use this information to determine how much to bid themselves. This competition leads to higher bids.
On the other hand Dutch auctions are a little bit to complicate because to be effective a bidder must have some idea of how low the bidding will go before it is accepted. For example, if the bidding starts at $2000, then goes to $1900, then to $1800, the anxious bidder may go ahead and accept that price even though it could have went all the way to $1500 without being accepted.
Conclusions
[edit | edit source]The private value experiment is a good way to test theoretical assumption in practice. In both First and Second price auction with two bidders we have the same results of the overbidding of the participants. Participants are risk averse: by marginally increasing the bid, the agent lowers his profit if he wins (hence, increasing the seller’s revenue), but increases the probability of his winning. Moreover they do not know other bidders' private value in a private value auction. As a result they tend to bid higher than they normally should.
We tried to identify if the number of the participants who act as bidders affects our results. We added bidders and we had almost the same results as before with only two bidders. The participants again start to bid more than the optimal bid and many times they overbid even their private value. It seems that the number of bidders affects the decisions of the participants in such way, that they are willing to bid more. Because of the higher competition for the good, players sacrifice their return in order to increase the probability of winning the auction.
References
[edit | edit source]- Gneezy U & Smorodinsky, R (2005): All-pay auctions an experimental study. Forthcoming Publication Journal of Economic behavior and organization.
- Holt , Charles A. &, A.E. Roth( 2004): The Nash equilibrium - A perspective. PNAS vol 101,no12 p. 3999-4002.
- Kagel, J. & Levin. D. (1993): Independent Private Value auctions: Bidder Behavior in First-Second and Third Price Auctions with Varying numbers of Bidders. Economic Journal Vol. 103 p.2-5.
- Kagel, J. and A.E. Roth(1995): Handbook of Experimental economics. Princeton University Press, Princeton.
- Milgrom, P. (1998:, Putting Auction Theory to work, forthcoming. Cambridge University Press.
- Osborne, Martin J. (2004): An Introduction to Game Theory. Oxford: Oxford University Press Oxford.
- An Online Second Price Auction Game (2nd game in the list).
| Topics in Economic Classroom Experiments | |
|
Auctions |
|
|
Markets |
|
|
Public Economics |
|
|
Industrial Organization |
|
|
Macroeconomics and Finance |
|
|
Game Theory |
|
|
Individual Decisions |
|






![{\displaystyle [0,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af219c8f0e8e0381e7b35e63dd7093e86d83a540)