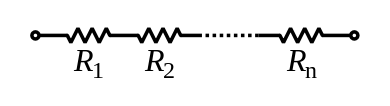Electronics Fundamentals/Lecture Resistors and Ohms law

The Electronic Circuit

Every electronic circuit has 2 basic parts and can be eventually broken down to these 2 parts. The power supply V1, and the load R1, in this example.

V1 R1

We have many different measurements, feet, inches, centimeters, meters, miles, kilometers, liters, cups, ounces, grams, pounds. In this lecture we will teach you the basic measurements for electronics Volts, Amps, Ohms, Watts, Frequency, Farads, Henrys, Gaussen, Telsas. Lets start with Volts, Amps, Watts.

Watts law

You are all familiar with the light bulb. In the basic household circuit your fuse box is the power supply, and the light bulb is the load, or V1 and R1 in our schematic.

Given Watts law you can figure out many other measurements based on this.

$V\times I=W\!$ or $W/I=V\!$ or $W/V=I\!$

Which now gives you the ability to derive Volts, Watts or Amps from any of the other 2.

+ voltage - resistance ←current flow

todo switch circuit using household wiring diagrams

Lets say the bulbs wattage is 60W. Lets also say that we are in north America and the standard is 120Volts. Given the above we can find the current draw or AMPs drawn by the lamp. I is current V is voltage W is wattage. The resulting equation is $W/V=I\!$ or $60W/120V=.5A\!$

+ 120 VAC RMS     - resistance ←→ .5A

TODO practical justification for where this is used
TODO more examples sovle for watts solve for volts practial resons why these are needed
TODO 6 practice problems 2 for each equation and hidden answers

Ohms Law

Ohm's law applies to electrical circuits; it states that the current through a conductor between two points is directly proportional to the potential difference (i.e. voltage drop or voltage) across the two points, and inversely proportional to the resistance(Ohms) between them. the symbol for ohm is $\Omega \!$ and the equation is $V=I\times R\!$

+ 120 VAC RMS     - resistance ←→ .5A

So now lets figure out the resistance of our 60W bulb. We have already figured the current flowing thrue the bulb, and we already knew that we have 120V and a 60W bulb at 120V.
we know the voltage and we know the current so we need to alter the equation a little.

$V=I\times R\!$	$120Volts=.5Amps\times R\!$	We need to move I over. Divide I on both sides of the = to counter the multiplication.
${\cfrac {V}{I}}={\cfrac {I\times R}{I}}\!$	${\cfrac {120Volts}{.5Amps}}={\cfrac {.5\times R}{.5Amps}}\!$	Simplify.
${\cfrac {V}{I}}=R\!$	${\cfrac {120Volts}{.5Amps}}=R\!$

${\cfrac {120Volts}{.5Amps}}=R\!$ Which gets us.

${\cfrac {120Volts}{.5Amps}}=240\Omega \!$

+ 120 VAC RMS     - 240Ω 60W 120V ←→ .5A

As shown here, it is best to quote wattage requirements and voltage drop requirements on a resistor for all devices. To much info is never a problem, a lack of information will cost time and money, if someone suddenly needs it.

TODO practical justification for where this is used
TODO more examples solve for watts solve for volts practical reasons why these are needed
TODO 6 practice problems 2 for each equation and hidden answers

The Resistor

A resistor is a passive two-terminal electrical component that implements electrical resistance as a circuit element. The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's terminals to the intensity of current through the circuit is called resistance.

From http://en.wikipedia.org/wiki/Resistor#Series_and_parallel_resistors as of 03-27-2012

Resistors in Series

In a series configuration, the current through all of the resistors is the same, but the voltage across each resistor will be in proportion to its resistance. The potential difference (voltage) seen across the network is the sum of those voltages, thus the total resistance can be found as the sum of those resistances:

$R_{\mathrm {eq} }=R_{1}+R_{2}+\cdots +R_{n}$

As a special case, the resistance of N resistors connected in series, each of the same resistance R, is given by NR.

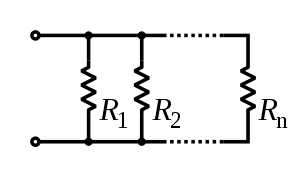
Resistors in parallel

Resistors in a parallel configuration are each subject to the same potential difference (voltage), however the currents through them add. The conductances of the resistors then add to determine the conductance of the network. Thus the equivalent resistance (R_eq) of the network can be computed:

${\frac {1}{R_{\mathrm {eq} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}$

The parallel equivalent resistance can be represented in equations by two vertical lines "||" (as in geometry) as a simplified notation. Occasionally two slashes "//" are used instead of "||", in case the keyboard or font lacks the vertical line symbol. For the case of two resistors in parallel, this can be calculated using:

$R_{\mathrm {eq} }=R_{1}\|R_{2}={R_{1}R_{2} \over R_{1}+R_{2}}$