Dynamics/Kinematics/Reference Frames

Introduction

Content taken from Frame of reference and Inertial frame of reference

In physics, a frame of reference (or reference frame) consists of an abstract coordinate system and the set of physical reference points that uniquely fix (locate and orient) the coordinate system and standardize measurements within that frame.

For n dimensions, n + 1 reference points are sufficient to fully define a reference frame. Using rectangular (Cartesian) coordinates, a reference frame may be defined with a reference point at the origin and a reference point at one unit distance along each of the n coordinate axes.

"Different" Reference Frames

The need to distinguish between the various meanings of "frame of reference" has led to a variety of terms. For example, sometimes the type of coordinate system is attached as a modifier, as in Cartesian frame of reference. Sometimes the state of motion is emphasized, as in rotating frame of reference.

The term observational frame of reference is used when emphasis is upon the state of motion rather than upon the coordinate choice or the character of the observations or observational apparatus. In this sense, an observational frame of reference allows study of the effect of motion upon an entire family of coordinate systems that could be attached to this frame. On the other hand, a coordinate system may be employed for many purposes where the state of motion is not the primary concern. Observational frames of reference, coordinate systems, and observational equipment are independent concepts, separated as below:

• An observational frame (such as an inertial frame or non-inertial frame of reference) is a physical concept related to state of motion.
• A coordinate system is a mathematical concept, amounting to a choice of language used to describe observations.

In very general terms, a coordinate system is a set of arcs xⁱ = xⁱ(t) in a complex Lie group. Less abstractly, a coordinate system in a space of n-dimensions is defined in terms of a basis set of vectors {e₁, e₂,… e_n}. As such, the coordinate system is a mathematical construct, a language, that may be related to motion, but has no necessary connection to motion. Consequently, an observer in an observational frame of reference can choose to employ any coordinate system (Cartesian, polar, curvilinear, generalized, …) to describe observations made from that frame of reference. A change in the choice of this coordinate system does not change an observer's state of motion, and so does not entail a change in the observer's observational frame of reference. This viewpoint can be found elsewhere as well. Which is not to dispute that some coordinate systems may be a better choice for some observations than are others.

• Choice of what to measure and with what observational apparatus is a matter separate from the observer's state of motion and choice of coordinate system.

Here is a quotation applicable to moving observational frames ${\mathfrak {R}}$ and various associated Euclidean three-space coordinate systems [R, R′, etc.]:

“ We first introduce the notion of reference frame, itself related to the idea of observer: the reference frame is, in some sense, the "Euclidean space carried by the observer". Let us give a more mathematical definition:… the reference frame is... the set of all points in the Euclidean space with the rigid body motion of the observer. The frame, denoted ${\mathfrak {R}}$, is said to move with the observer.… The spatial positions of particles are labelled relative to a frame ${\mathfrak {R}}$ by establishing a coordinate system R with origin O. The corresponding set of axes, sharing the rigid body motion of the frame ${\mathfrak {R}}$, can be considered to give a physical realization of ${\mathfrak {R}}$. In a frame ${\mathfrak {R}}$, coordinates are changed from R to R′ by carrying out, at each instant of time, the same coordinate transformation on the components of intrinsic objects (vectors and tensors) introduced to represent physical quantities in this frame. ”

and this on the utility of separating the notions of ${\mathfrak {R}}$ and [R, R′, etc.]:

“ As noted by Brillouin, a distinction between mathematical sets of coordinates and physical frames of reference must be made. The ignorance of such distinction is the source of much confusion… the dependent functions such as velocity for example, are measured with respect to a physical reference frame, but one is free to choose any mathematical coordinate system in which the equations are specified. ”

and this, also on the distinction between ${\mathfrak {R}}$ and [R, R′, etc.]:

“ The idea of a reference frame is really quite different from that of a coordinate system. Frames differ just when they define different spaces (sets of rest points) or times (sets of simultaneous events). So the ideas of a space, a time, of rest and simultaneity, go inextricably together with that of frame. However, a mere shift of origin, or a purely spatial rotation of space coordinates results in a new coordinate system. So frames correspond at best to classes of coordinate systems. ”

and from J. D. Norton:

“ In traditional developments of special and general relativity it has been customary not to distinguish between two quite distinct ideas. The first is the notion of a coordinate system, understood simply as the smooth, invertible assignment of four numbers to events in spacetime neighborhoods. The second, the frame of reference, refers to an idealized system used to assign such numbers […] To avoid unnecessary restrictions, we can divorce this arrangement from metrical notions. […] Of special importance for our purposes is that each frame of reference has a definite state of motion at each event of spacetime. […] Within the context of special relativity and as long as we restrict ourselves to frames of reference in inertial motion, then little of importance depends on the difference between an inertial frame of reference and the inertial coordinate system it induces. This comfortable circumstance ceases immediately once we begin to consider frames of reference in nonuniform motion even within special relativity.…More recently, to negotiate the obvious ambiguities of Einstein’s treatment, the notion of frame of reference has reappeared as a structure distinct from a coordinate system. ”

Coordinate Systems for Reference Frames

An observer O, situated at the origin of a local set of coordinates – a frame of reference F. The observer in this frame uses the coordinates (x, y, z, t) to describe a spacetime event, shown as a star.

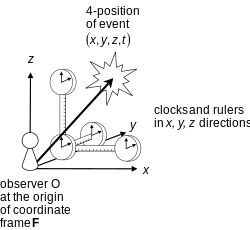
The coordinates of a point r in an n-dimensional space are simply an ordered set of n numbers:

$\mathbf {r} =[x^{1},\ x^{2},\ \dots ,\ x^{n}].$

In a physical problem, they could be spacetime coordinates or normal mode amplitudes. In a robot design, they could be angles of relative rotations, linear displacements, or deformations of joints. Here we will suppose these coordinates can be related to a Cartesian coordinate system by a set of functions:

$x^{j}=x^{j}(x,\ y,\ z,\ \dots ),\quad j=1,\ \dots ,\ n,$

where x, y, z, etc. are the n Cartesian coordinates of the point. Given these functions, coordinate surfaces are defined by the relations:

$x^{j}(x,y,z,\dots )=\mathrm {constant} ,\quad j=1,\ \dots ,\ n.$

The intersection of these surfaces define coordinate lines. At any selected point, tangents to the intersecting coordinate lines at that point define a set of basis vectors {e₁, e₂, …, e_n} at that point. That is:

$\mathbf {e} _{i}(\mathbf {r} )=\lim _{\epsilon \rightarrow 0}{\frac {\mathbf {r} \left(x^{1},\ \dots ,\ x^{i}+\epsilon ,\ \dots ,\ x^{n}\right)-\mathbf {r} \left(x^{1},\ \dots ,\ x^{i},\ \dots ,\ x^{n}\right)}{\epsilon }},\quad i=1,\ \dots ,\ n,$

which can be normalized to be of unit length.

Coordinate surfaces, coordinate lines, and basis vectors are components of a coordinate system. If the basis vectors are orthogonal at every point, the coordinate system is an orthogonal coordinate system.

As is apparent from these remarks, a coordinate system is a mathematical construct, part of an axiomatic system. There is no necessary connection between coordinate systems and physical motion (or any other aspect of reality). However, coordinate systems can include time as a coordinate, and can be used to describe motion.

Observational frames of reference

Three frames of reference in special relativity. The black frame is at rest. The primed frame moves at 40% of light speed, and the double primed frame at 80%. Note the scissors-like change as speed increases.

An observational frame of reference, often referred to as a physical frame of reference, a frame of reference, or simply a frame, is a physical concept related to an observer and the observer's state of motion. Here we adopt the view expressed by Kumar and Barve: an observational frame of reference is characterized only by its state of motion. However, there is lack of unanimity on this point.

There are two types of observational reference frame: inertial and non-inertial. An inertial frame of reference is defined as one in which all laws of physics take on their simplest form. In Newtonian mechanics, a more restricted definition requires only that Newton's first law holds true; that is, a Newtonian inertial frame is one in which a free particle travels in a straight line at constant speed, or is at rest.

In contrast to the inertial frame, a non-inertial frame of reference is one in which fictitious forces must be invoked to explain observations. An example is an observational frame of reference centered at a point on the Earth's surface. This frame of reference orbits around the center of the Earth, which introduces the fictitious forces known as the Coriolis force, centrifugal force, and gravitational force. (All of these forces including gravity disappear in a truly inertial reference frame, which is one of free-fall.)

Examples of inertial frames of reference

Simple example

Figure 1: Two cars moving at different but constant velocities observed from stationary inertial frame S attached to the road and moving inertial frame S′ attached to the first car.

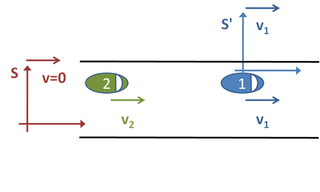
Consider a situation common in everyday life. Two cars travel along a road, both moving at constant velocities. See Figure 1. At some particular moment, they are separated by 200 metres. The car in front is travelling at 22 metres per second and the car behind is travelling at 30 metres per second. If we want to find out how long it will take the second car to catch up with the first, there are three obvious "frames of reference" that we could choose.

First, we could observe the two cars from the side of the road. We define our "frame of reference" S as follows. We stand on the side of the road and start a stop-clock at the exact moment that the second car passes us, which happens to be when they are a distance d = 200 m apart. Since neither of the cars is accelerating, we can determine their positions by the following formulas, where $x_{1}(t)$ is the position in meters of car one after time t in seconds and $x_{2}(t)$ is the position of car two after time t.

$x_{1}(t)=d+v_{1}t=200+22t,\quad x_{2}(t)=v_{2}t=30t.$

Notice that these formulas predict at t = 0 s the first car is 200 m down the road and the second car is right beside us, as expected. We want to find the time at which $x_{1}=x_{2}$. Therefore, we set $x_{1}=x_{2}$ and solve for $t$, that is:

$200+22t=30t,$

$8t=200,$

$t=25\ \mathrm {seconds} .$

Alternatively, we could choose a frame of reference S′ situated in the first car. In this case, the first car is stationary and the second car is approaching from behind at a speed of v₂ − v₁ = 8 m/s. In order to catch up to the first car, it will take a time of d/v₂ − v₁ = 200/8 s, that is, 25 seconds, as before. Note how much easier the problem becomes by choosing a suitable frame of reference. The third possible frame of reference would be attached to the second car. That example resembles the case just discussed, except the second car is stationary and the first car moves backward towards it at 8 m/s.

It would have been possible to choose a rotating, accelerating frame of reference, moving in a complicated manner, but this would have served to complicate the problem unnecessarily. It is also necessary to note that one is able to convert measurements made in one coordinate system to another. For example, suppose that your watch is running five minutes fast compared to the local standard time. If you know that this is the case, when somebody asks you what time it is, you are able to deduct five minutes from the time displayed on your watch in order to obtain the correct time. The measurements that an observer makes about a system depend therefore on the observer's frame of reference (you might say that the bus arrived at 5 past three, when in fact it arrived at three).

Additional example

Figure 2: Simple-minded frame-of-reference example

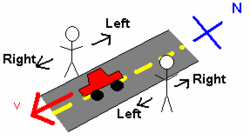
For a simple example involving only the orientation of two observers, consider two people standing, facing each other on either side of a north-south street. See Figure 2. A car drives past them heading south. For the person facing east, the car was moving towards the right. However, for the person facing west, the car was moving toward the left. This discrepancy is because the two people used two different frames of reference from which to investigate this system.

For a more complex example involving observers in relative motion, consider Alfred, who is standing on the side of a road watching a car drive past him from left to right. In his frame of reference, Alfred defines the spot where he is standing as the origin, the road as the x-axis and the direction in front of him as the positive y-axis. To him, the car moves along the x axis with some velocity v in the positive x-direction. Alfred's frame of reference is considered an inertial frame of reference because he is not accelerating (ignoring effects such as Earth's rotation and gravity).

Now consider Betsy, the person driving the car. Betsy, in choosing her frame of reference, defines her location as the origin, the direction to her right as the positive x-axis, and the direction in front of her as the positive y-axis. In this frame of reference, it is Betsy who is stationary and the world around her that is moving – for instance, as she drives past Alfred, she observes him moving with velocity v in the negative y-direction. If she is driving north, then north is the positive y-direction; if she turns east, east becomes the positive y-direction.

Finally, as an example of non-inertial observers, assume Candace is accelerating her car. As she passes by him, Alfred measures her acceleration and finds it to be a in the negative x-direction. Assuming Candace's acceleration is constant, what acceleration does Betsy measure? If Betsy's velocity v is constant, she is in an inertial frame of reference, and she will find the acceleration to be the same as Alfred in her frame of reference, a in the negative y-direction. However, if she is accelerating at rate A in the negative y-direction (in other words, slowing down), she will find Candace's acceleration to be a′ = a − A in the negative y-direction—a smaller value than Alfred has measured. Similarly, if she is accelerating at rate A in the positive y-direction (speeding up), she will observe Candace's acceleration as a′ = a + A in the negative y-direction—a larger value than Alfred's measurement.

Non-inertial frames

Here the relation between inertial and non-inertial observational frames of reference is considered. The basic difference between these frames is the need in non-inertial frames for fictitious forces, as described below.

An accelerated frame of reference is often delineated as being the "primed" frame, and all variables that are dependent on that frame are notated with primes, e.g. x′, y′, a′.

The vector from the origin of an inertial reference frame to the origin of an accelerated reference frame is commonly notated as R. Given a point of interest that exists in both frames, the vector from the inertial origin to the point is called r, and the vector from the accelerated origin to the point is called r′. From the geometry of the situation, we get

$\mathbf {r} =\mathbf {R} +\mathbf {r} '.$

Taking the first and second derivatives of this with respect to time, we obtain

$\mathbf {v} =\mathbf {V} +\mathbf {v} ',$

$\mathbf {a} =\mathbf {A} +\mathbf {a} '.$

where V and A are the velocity and acceleration of the accelerated system with respect to the inertial system and v and a are the velocity and acceleration of the point of interest with respect to the inertial frame.

These equations allow transformations between the two coordinate systems; for example, we can now write Newton's second law as

$\mathbf {F} =m\mathbf {a} =m\mathbf {A} +m\mathbf {a} '.$

When there is accelerated motion due to a force being exerted there is manifestation of inertia. If an electric car designed to recharge its battery system when decelerating is switched to braking, the batteries are recharged, illustrating the physical strength of manifestation of inertia. However, the manifestation of inertia does not prevent acceleration (or deceleration), for manifestation of inertia occurs in response to change in velocity due to a force. Seen from the perspective of a rotating frame of reference the manifestation of inertia appears to exert a force (either in centrifugal direction, or in a direction orthogonal to an object's motion, the Coriolis effect).

A common sort of accelerated reference frame is a frame that is both rotating and translating (an example is a frame of reference attached to a CD which is playing while the player is carried). This arrangement leads to the equation (see Fictitious force for a derivation):

$\mathbf {a} =\mathbf {a} '+{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '+2{\boldsymbol {\omega }}\times \mathbf {v} '+{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')+\mathbf {A} _{0},$

or, to solve for the acceleration in the accelerated frame,

$\mathbf {a} '=\mathbf {a} -{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '-2{\boldsymbol {\omega }}\times \mathbf {v} '-{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')-\mathbf {A} _{0}.$

Multiplying through by the mass m gives

$\mathbf {F} '=\mathbf {F} _{\mathrm {physical} }+\mathbf {F} '_{\mathrm {Euler} }+\mathbf {F} '_{\mathrm {Coriolis} }+\mathbf {F} '_{\mathrm {centripetal} }-m\mathbf {A} _{0},$

where

$\mathbf {F} '_{\mathrm {Euler} }=-m{\dot {\boldsymbol {\omega }}}\times \mathbf {r} '$ (Euler force),

$\mathbf {F} '_{\mathrm {Coriolis} }=-2m{\boldsymbol {\omega }}\times \mathbf {v} '$ (Coriolis force),

$\mathbf {F} '_{\mathrm {centrifugal} }=-m{\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times \mathbf {r} ')=m(\omega ^{2}\mathbf {r} '-({\boldsymbol {\omega }}\cdot \mathbf {r} '){\boldsymbol {\omega }})$ (centrifugal force).

Particular frames of reference in common use

• International Terrestrial Reference Frame
• International Celestial Reference Frame
• In fluid mechanics, Lagrangian and Eulerian specification of the flow field