Dynamics/Kinematics/Coordinate Systems/Cartesian
Introduction
[edit | edit source]Content from Cartesian coordinate system
A Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference line is called a coordinate axis or just axis (plural axes) of the system, and the point where they meet is its origin, at ordered pair (0, 0). The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin.
Two dimensions
[edit | edit source]
A Cartesian coordinate system in two dimensions (also called a rectangular coordinate system or an orthogonal coordinate system[1]) is defined by an ordered pair of perpendicular lines (axes), a single unit of length for both axes, and an orientation for each axis. The point where the axes meet is taken as the origin for both, thus turning each axis into a number line. For any point P, a line is drawn through P perpendicular to each axis, and the position where it meets the axis is interpreted as a number. The two numbers, in that chosen order, are the Cartesian coordinates of P. The reverse construction allows one to determine the point P given its coordinates.
The first and second coordinates are called the abscissa and the ordinate of P, respectively; and the point where the axes meet is called the origin of the coordinate system. The coordinates are usually written as two numbers in parentheses, in that order, separated by a comma, as in (3, −10.5). Thus the origin has coordinates (0, 0), and the points on the positive half-axes, one unit away from the origin, have coordinates (1, 0) and (0, 1).
Three Dimensions
[edit | edit source]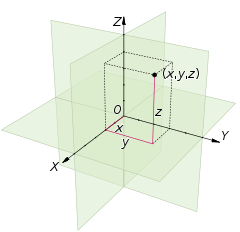
A Cartesian coordinate system for a three-dimensional space consists of an ordered triplet of lines (the axes) that go through a common point (the origin), and are pair-wise perpendicular; an orientation for each axis; and a single unit of length for all three axes. As in the two-dimensional case, each axis becomes a number line. For any point P of space, one considers a hyperplane through P perpendicular to each coordinate axis, and interprets the point where that hyperplane cuts the axis as a number. The Cartesian coordinates of P are those three numbers, in the chosen order. The reverse construction determines the point P given its three coordinates.
Translation and Rotation in Two Dimensions
[edit | edit source]Translation
[edit | edit source]Translating a set of points of the plane, preserving the distances and directions between them, is equivalent to adding a fixed pair of numbers (a, b) to the Cartesian coordinates of every point in the set. That is, if the original coordinates of a point are (x, y), after the translation they will be
Rotation
[edit | edit source]To rotate a figure counterclockwise around the origin by some angle is equivalent to replacing every point with coordinates (x,y) by the point with coordinates (x',y'), where
Thus:
Position
[edit | edit source]One notation for representing position is the following:[2]
Velocity
[edit | edit source]One notation for representing velocity is the following:[2]
Acceleration
[edit | edit source]One notation for representing velocity is the following:[2]
References
[edit | edit source]- ↑ Bix, Robert A.; D'Souza, Harry J. "Analytic geometry". Encyclopædia Britannica. Retrieved 2017-08-06.
- ↑ 2.0 2.1 2.2 Baruh, Haim (2014). Applied Dynamics. p. 31. doi:10.1201/b17897. http://dx.doi.org/10.1201/b17897.








