Classic energy problem in open-channel flow

Specific energy is the amount of energy per weight of the fluid with the channel bed considered as the datum. The specific energy of water in a channel is the summation of the dynamic pressure head and the static pressure head. In the case where the datum is the channel bed, the static pressure head or the hydraulic head is just simply the flow depth, denoted by y. This article presents the application of a specific classic energy problem in open-channel flow.

$E=y+{\frac {v^{2}}{2g}}\,\!$

Where:	E = specific energy (length)
	${\frac {v^{2}}{2g}}\,\!$ = dynamic pressure head (length)
	y = static pressure head = flow depth (length)

The specific energy is extremely useful in in understanding the flow characteristics at flow transitions like constrictions, expansions, steps, and sluice gates. The application can potentially also extend to that of the studying the effects of bedforms such as dunes and most open channel flow measurement devices like weirs which have some basis on the consideration of energy in the fluid. The classical energy problems in the discussion presented herein aim to familiarize the concept of specific energy and the resulting flow characteristics through the use of equations and graphically on an energy depth diagram.

Lowering of sluice gate in an open-channel flow

• A sluice gate is lowered into a rectangular channel. The velocity of flow and specific energy upstream is 2.0 m/s and 2.2 m respectively. How will the depths upstream and downstream of sluice gate change when the sluice gate is lowered:

1. To a height that is above critical depth of the flow? : (gate opening = 1.40 m)
2. Below critical depth of the flow? : (gate opening = 0.8 m)
3. Below supercritical alternate depth of the upstream flow? : (gate opening = 0.5 m)

Lowering of sluice gate in an open channel flow

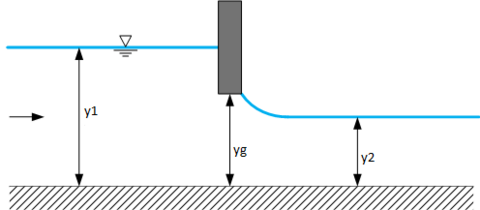
Solution:

Step1:Before starting to solve the question, it is always better to have the values of unit discharge(q) and corresponding critical depth(y_c)known.Since specific energy upstream (E_u/p)of the flow is given, we will with the help of energy depth relationship first out the depth of the flow upstream (y₁). Then we can proceed finding the unit discharge (q)and the critical depth(y_c) of the above flow.

$E_{u/p}=y_{1}+{\frac {v^{2}}{2g}}\,\!$ $2.2=y_{1}+{\frac {2^{2}}{2(9.8)}}$ Solving, we get depth upstream (y1) = 2.0 m

Step2: Unit discharge or discharge per unit width(q) given by:

$q=(v\times y_{1})=(2\times 2)=4.0{\text{ m}}^{2}/s$

Step3: Critical depth(y_c) or the depth for which the above flow has minimum specific energy:

$y_{c}={\biggl (}{\frac {q^{2}}{g}}{\biggr )}^{\frac {1}{3}}={\biggl (}{\frac {(4.00)^{2}}{9.81}}{\biggr )}^{\frac {1}{3}}=1.18m$ Since, depth upstream (y1) is greater than the critical depth (yc), flow upstream is subcritical.

Step4: When the sluice gate is kept above the critical depth of flow, the depth downstream will remain same as depth upstream. The flow does not have an accessible pathway to supercritical flow. Therefore for the part(1) of the question, the sluice gate is just getting wet and depth downstream (y₂) :

$y_{2}=y_{1}=2.0m$

Step5: In part(2) of the question the sluice gate is lowered below the critical depth of the flow. So here, the flow does have an accessible pathway to supercritical flow. The depth downstream (y₂)of the sluice gate will be alternate to upstream depth (y₁).We will use the alternate depth equation to determine (y₂) given (y₁) and the unit discharge, q.

$y_{2}={\frac {2y_{1}}{-1+{\sqrt {1+{\frac {8gy_{1}^{3}}{q^{2}}}}}}}={\frac {(2)(2)}{-1+{\sqrt {1+{\frac {8(9.8)(2)^{3}}{4^{2}}}}}}}=0.75m$ Therefore the depth downstream of sluice gate (y2) = 0.75m

Step6: In part (3) of the question, the gate opening (y_g)is kept below the super-critical alternate depth of flow. Therefore the gate now represents a choke condition and depth upstream now will increase. Just when the choked flow conditions are developed, the instantaneous unit discharge or the transient discharge (q_trans)passing through the gate will be given by:

$y_{g}+{\frac {q_{\mathrm {trans} }^{2}}{2gy_{g}^{2}}}=E_{u/p}$ $0.5+{\frac {q_{\mathrm {trans} }^{2}}{2(9.8)(.5^{2})}}=2.20$ Solving, we get the transient discharge passing through the gate (qtrans) = 2.89 m2/s

Step7: At steady state conditions, the unit discharge passing through the gate will be the same as originally specified. Now the depth upstream will be different and will be alternate depth to the gate opening (y_g).

$y_{1}={\frac {2y_{g}}{-1+{\sqrt {1+{\frac {8gy_{g}^{3}}{q^{2}}}}}}}={\frac {(2)(0.5)}{-1+{\sqrt {1+{\frac {8(9.8)(0.5)^{3}}{4^{2}}}}}}}=3.71{\text{ m}}$ Therefore, the new depth upstream is = 3.71 m which is greater than the initial depth of 2.0 m.

The corresponding Energy-Depth diagram for this question has been plotted and shown below: Lowering of sluice gate in a subcritical flow

• An algorithm for solving similar questions in a subcritical flow :

By using the specific energy equation,calculate the depth upstream of the flow→ Find out the unit discharge flowing through the gate→ Find out the value of critical depth (y_c).→ From the alternate depth formula, find out the depth value alternate to upstream depth→ Compare the value of gate opening (y_g) with the critical depth (y_c) and alternate depth (y_alt)→ If (y_g)is greater than (y_c), depth upstream and downstream remains the same→ if (y_g) lies between critical depth (y_c)and alternate depth (y_alt), then the depth downstream of gate is (y_alt)and upstream flow depth remains the same→ if (y_g) is even less than (y_alt), then depth downstream of gate will be same as (y_g) and depth upstream will increase to a value which will be alternate to (y_g).

• Consider the case, when the sluice gate is lowered into a supercritical in a rectangular channel.The gate opening is kept at 0.30m. The velocity of flow and specific energy upstream is 10.0 m/s and 5.47 m respectively. How will the depths upstream and downstream of sluice gate change in this situation?

Solution:

The instant the gate touches the supercritical flow; it will force a downstream depth equal to the opening of the gate. This means that the flow now requires more specific energy than what it had initially. Therefore, it's a choke. As a result, now we will see a hydraulic jump upstream of the gate. The depth immediately upstream of the gate will now be the subcritical alternate depth to the downstream depth which is equal to the gate opening.

Step1: Finding the initial depth upstream of the flow:

$E_{u/p}=y_{1}+{\frac {v^{2}}{2g}}\,\!$ $5.47=y_{1}+{\frac {10.0^{2}}{2(9.81)}}$ Solving, we get depth upstream (y1) = 0.37 m

Step2: Unit discharge or discharge per unit width(q) given by:

$q=(v\times y_{1})=(10\times 0.37)=3.7{\text{ m}}^{2}/{\text{s}}$

Step3:After the sluice gate is lowered to a height of 0.4m and steady state conditions are achieved, New depth upstream will be given by :

$y_{1}={\frac {2y_{g}}{-1+{\sqrt {1+{\frac {8gy_{g}^{3}}{q^{2}}}}}}}={\frac {(2)(0.30)}{-1+{\sqrt {1+{\frac {8(9.8)(0.30)^{3}}{3.70^{2}}}}}}}=8.04{\text{ m}}$ Therefore, the new depth upstream is = 5.47 m which is greater than the initial depth of 0.5 m.

An algorithm for solving similar questions in a supercritical flow:

By using the specific energy equation,calculate the depth upstream of the flow→ Find out the unit discharge flowing through the gate→ When the sluice gate touches the flow and is lowered down to a depth(y_g), choke conditions will be developed→ The flow will back up upstream to a subcritical depth → Depth upstream (y_u/s) will now be alternate depth to (y_g).→ Depth downstream flow will be equal to the gate opening.

Constriction in an open-channel flow due to smooth narrowing of the channel width

As the word constriction suggests, the channel width in an open-channel flow reduces in size and that leads the flow to change its characteristics from the upstream values. Let’s consider the following question to understand the concept better.

• An open rectangular channel in the city of Blacksburg carries a constant discharge of 20.0 ft³/s at a depth of 3.0 ft. The width of the channel upstream and downstream is 4.0 ft and 2.0 ft respectively. Considering this transition to be smooth and the flow to be frictionless,

1. Determine the water surface elevation in the constriction.
2. If instead of 2.0 ft, the width of the channel is reduced to 1.0 ft, would upstream flow undergo any changes in its depth?
3. What is the maximum reduction that one can make in the width of the channel for upstream flow to remain same as before?

Solution:

Top view of constriction in a channel

Step1: Froude number of the upstream flow :

$Fr={\frac {q}{\sqrt {gy^{3}}}}={\frac {5}{\sqrt {32.2(3^{3})}}}=0.17{\text{ (subcritical flow)}}$

Step2: Specific energy of upstream flow (E_u/p):

$E_{u/p}=y_{1}+{\frac {q_{1}^{2}}{2gy_{1}^{2}}}=3+{\frac {5^{2}}{2(32.2)(3^{2})}}=3.04ft$

Step3: Corresponding to this upstream specific energy,the maximum discharge (q_max) possible:

$q_{\max }={\sqrt {(E_{u}^{3})(g) \over (1.5)^{3}}}={\sqrt {(3.04^{3})(32.2) \over (1.5)^{3}}}=16.4{\text{ ft}}^{2}/s$

Step4: The minimum width(W_min)allowed downstream so that upstream flow depth remains unchanged:

$W_{\min }={\frac {Q}{q_{\max }}}={\frac {20}{16.4}}=1.22{\text{ ft}}$

Step5:In part (i) of the question, the width(W_d/s)reduces to 2 ft which is greater than W_min. Therefore the flow depth remains unchanged upstream. Also here discharge per unit width in the constriction (q₂) :

$q_{2}={\frac {Q}{W_{d/s}}}={\frac {20}{2}}=10.0{\text{ ft}}^{2}/s$

Step6: Since flow is frictionless, the specific energy remains conserved both upstream (E_u/p) and on the constriction (E_d/s):

$E_{u/p}=E_{d/s}\,\!$ $3.04=y_{2}+{\frac {q_{2}^{2}}{2gy_{2}^{2}}}$ $3.04=y_{2}+{\frac {10^{2}}{2(32.2)y_{2}^{2}}}$ Solving we get depth on constriction, y2 = 2.85 ft and y2 is less than y1 .Therefore for a constriction in a subcritical flow the depth downstream decreases.

Step7: In part (2) of the question, new Width(W_d/s) = 1.0 ft which is less than the W_min. It’s a choke and the upstream flow conditions will change.

Step8: New downstream discharge (q₃)on constriction per unit width:

$q_{3}={\frac {Q}{W_{d/s}}}={\frac {20}{1}}=20{\text{ ft}}^{2}/s$

Step9: Specific energy of the downstream flow (E_d/s) will be equal to the critical specific energy corresponding to the new (q₃):

$E_{d/s}=(1.5){\biggl (}{\frac {q_{3}^{2}}{g}}{\biggr )}^{\frac {1}{3}}=(1.5){\biggl (}{\frac {20^{2}}{32.2}}{\biggr )}^{\frac {1}{3}}=3.47{\text{ ft}}$

Step10: To find the new depth upstream and downstream(y₁), again apply the concept of specific energy conservation upstream and downstream :

$E_{u/p}=E_{d/s}\,\!$ $y_{1}+{\frac {q_{1}^{2}}{2gy_{1}^{2}}}=3.47$ $y_{1}+{\frac {5^{2}}{2(32.2)(y_{1}^{2})}}=3.47$ Solving we get new depth upstream , y1 = 3.44ft. $y_{2}=y_{c}={\frac {2}{3}}E_{c}={\frac {2}{3}}(3.47)=2.31$ Solving we get new depth downstream , y2 = 2.31ft.

Step11: The initial transient discharge downstream (q_trans) when the flow just encounters the choke conditions, will be the "maximum discharge corresponding to the original upstream specific energy q_max = 16.4ft²/s." Correspondingly, the initial transient depth (y₂)on constriction downstream will be the critical depth given by :

$y_{c}={\biggl (}{\frac {q_{\mathrm {trans} }^{2}}{g}}{\biggr )}^{\frac {1}{3}}={\biggl (}{\frac {(16.4)^{2}}{(32.2)}}{\biggr )}^{\frac {1}{3}}=2.02{\text{ ft}}$

an algorithm for solving any such similar questions:

From the given value of unit discharge and depth, find the Fr number of upstream flow → Find out the upstream flow specific energy → corresponding to this specific energy, find out the maximum discharge possible (q_max)→ corresponding to this q_max, find out the minimum width (w_min) applicable for no choke condition = (Q/q_max)→ Compare this (w_min)with the given widths in question → If the given Width (W) of the constriction is greater than the w_min, then no choke conditions developed → If the given Width(W) of the constriction is less than w_min, choke conditions certainly developed and the upstream flow will encounter a change in its depth.→ Draw a rough E-y diagram (both for upstream and downstream). Since q upstream is different than q downstream, we will be having different E-y curves for upstream and downstream flow.

The corresponding Energy -Depth diagram has been plotted and shown below: constriction in an open channel flow

Expansion of the channel width in an open-channel flow

• Consider the same channel as above, however instead of reducing the width, the width is increased to 6.0 ft.

1. Assuming the transition to be smooth and frictionless, What will be the new surface water elevation downstream ?
2. Will the upstream flow conditions ever change for further increase in the width of the channel?

Solution:

Top view of channel expansion

Step1: Finding the Downstream discharge per unit width of the flow (q_d/s) :

$q_{d/s}={\frac {Q}{W_{d/s}}}={\frac {20}{6}}=3.33{\text{ ft}}^{2}/s$

Step2: Since the flow is considered to be frictionless,the specific energy remains same both upstream (E_u/p) and downstream (E_d/s):

$E_{u/p}=E_{d/s}\,\!$ $3.04=y_{2}+{\frac {q_{2}^{2}}{2gy_{2}^{2}}}$ $3.04=y_{2}+{\frac {(3.33)^{2}}{2(32.2)y_{2}^{2}}}$ Solving, we get depth on constriction, y2 = 3.03 ft.And y2 is greater than y1.

Therefore, in a subcritical flow, as the channel width increases the depth also increases downstream. The upstream flow conditions will never change due to further increase in the downstream width of the channel. Upstream flow conditions will change only when the downstream conditions cause a choke. Here, the flow upstream will always have sufficient energy to carry the flow downstream. So we will never encounter choke conditions in expansions.

• An algorithm for solving any such similar questions:

Calculate the unit discharge downstream (q_d/s). Since downstream, the channel width is increasing, value of (q_d/s) will be less than (q_u/p) → Since specific energy remains same in the case of expansion,(E_d/s) = (E_u/p)→ Using the energy depth formula, find out the depth downstream(y₂).→Roughly sketch out the E-y diagram for both upstream and downstream and realise that flow will never encounter choke conditions.

The Energy-Depth diagram for this question has been plotted and shown below: Expansion of channel width

An upward step in an open channel flow (rise in the channel bed)

• An open rectangular channel carrying a discharge of 10 ft²/s per unit width is flowing at a depth of 6.0 ft. After a certain distance the flow encounters a smooth step which makes the channel bed rise by 2.0 ft.

1. What will be the depth downstream of the step?
2. For an upward step of 4.0 ft, will the flow profile remain the same upstream? If not, then what would be the new upstream depth?

Solution:

Step1: For this question, the discharge per unit width (q = 10 ft²/s) remains same both upstream and downstream.

Froude number of upstream flow (Fr):

$Fr={\frac {q}{\sqrt {gy_{1}^{3}}}}={\frac {10}{\sqrt {32.2(6^{3})}}}=0.12{\text{ (subcritical flow)}}$

Step2: Specific energy of the flow upstream (E_u/p):

$E_{u/p}=y_{1}+{\frac {q^{2}}{2gy_{1}^{2}}}=6+{\frac {10^{2}}{2(32.2)(6^{2})}}=6.04{\text{ ft}}$

Step3: For q of 10 ft²/s, the minimum possible or the critical specific energy (E_c):

$E_{c}=(1.5){\biggl (}{\frac {q^{2}}{g}}{\biggr )}^{\frac {1}{3}}=(1.5){\biggl (}{\frac {10^{2}}{32.2}}{\biggr )}^{\frac {1}{3}}=2.20{\text{ ft}}$

Step4: Safe step: Maximum upward step (Z_max) possible for no choke conditions:

$(Z_{\max })=(E_{u/p}-E_{c})=(6.04-2.20)=3.84{\text{ ft}}\,\!$

Step5: For part (i) of the question, the upward step (Z) is equal to 2.0 ft which is less than the Z_max. Therefore, it’s not a choke and the upstream flow depth remains unchanged.

Step6: Specific energy of the flow on the step downstream (E_d/s):

$(E_{d/s})=(E_{u/p}-Z)=(6.04-2.0)=4.04ft\,\!$ $\Rightarrow (y_{2}+{\frac {q^{2}}{2gy_{2}^{2}}}=4.04ft)$ $\Rightarrow (y_{2}+{\frac {10^{2}}{2(32.2)(y_{2}^{2})}}=4.04)$ Solving, we get the depth on the step downstream (y2) = 3.95 ft.

Therefore from above working we conclude that for a subcritical flow, an upward step leads to decrease in the depth downstream of the flow

Step7: In part (ii) of the question, the upward step (Z) is equal to 4.0 ft which is greater than the Z_max. Therefore it’s a choke. The flow upstream will now need to change its depth to gather extra energy.

Step8: The specific energy downstream will be equal to critical specific energy (E_c) corresponding to discharge per unit width of 10 ft²/s as calculated in step 3 :

$E{d/s}=E_{c}=2.20{\text{ ft}}\,\!$

Step9: The specific energy upstream :

$(E_{u/p})=(E_{c}+Z)=(2.20+4)=6.20ft\,\!$ $\Rightarrow (y_{1}+{\frac {q^{2}}{2gy_{1}^{2}}}=6.20)$ $\Rightarrow (y_{1}+{\frac {10^{2}}{2(32.2)(y_{1}^{2})}}=6.20)$ Solving, we get the new depth upstream (y1) = 6.16 ft.

Step10: The initial transient discharge (q_trans) on the step,corresponding to the Original specific energy of the upstream flow:

$q_{\mathrm {trans} }={\sqrt {(E_{u/p}-Z)^{3}(g) \over (1.5)^{3}}}={\sqrt {(6.04-4)^{3}(g) \over (1.5)^{3}}}=9.00{\text{ ft}}^{2}/s$

* An algorithm for solving any such similar questions:

Calculate the froude number and find out whether the flow is subcritical or supercritical→ Find out the specific energy upstream→Since q remains the same for upstream & downstream, the q curve will be common to both upstream & downstream →Draw the E-y sketch and approximately show the specific energies and depths upstream & downstream (Safe step)→ find the critical energy corresponding to the given q→ When the step is less than (E_u/p − c) , it is not a choke→ When step is greater than (E_u/p − Ec) ,it is a choke.

The Energy-Depth diagram for this question has been plotted and shown below: An upward step in an open channel flow

A downward step in an open channel flow (fall in the channel bed)

• In the same channel as above, if the bed falls smoothly by 2.0 ft instead of a rise, then:

1. Find out the depth downstream.
2. Will the upstream depth ever change for further decrease in the bed level?

Solution:

Downward step in an open channel flow

Step1: Since it’s a downward step, the specific energy downstream (E_d/s)will be :

$(E_{d/s})=(E_{u/p}+Z)=(6.04+2)=8.04ft\,\!$ $\Rightarrow (y_{2}+{\frac {q^{2}}{2gy_{2}^{2}}}=8.04)$ $\Rightarrow (y_{2}+{\frac {10^{2}}{2(32.2)(y_{2}^{2})}}=8.04)$ Solving, we get the depth on the downward step (y2) = 8.04 ft.

Step2: Solving for part (ii) of the question, the upstream depth will never change for further decrease of the bed depth. Reason being : the specific energy downstream is always greater than the specific energy upstream. So the downstream conditions will never reach critical conditions.

• An algorithm for solving any such similar questions:

From the given value of q and depth, find out the specific energy of flow upstream(E_u/p)→ Add the value of downward step to (E_u/s)to obtain specific energy E_d/s)→ From specific energy-depth relationship, find out the value of depth downstream→Draw a rough E-y diagram showing the value of calculated depths and specific energies both upstream and downtream.→ since q remains same both upstream and downstream, E-y curve will be same for upstream flow as well as for downstream flow.

Energy depth diagram for this question has been plotted and shown below Downward step in an open channel flow

Combination problem: simultaneous constriction and negative step

PART A

An open rectangular channel carrying a discharge of 150 ft³/s is flowing at a depth of 3.75 ft with an energy of 4.00 ft and a width of 10 ft. The flow encounters a simultaneous gradual contraction to a width of 5 ft and a smooth downwards step of 2 ft. With these flow conditions:

1. Determine the minimum width that can pass the current flow.
2. Determine if the current conditions cause a choked flow.
3. Determine the depth of the downstream flow.
4. Determine if the downstream flow is subcritical or supercritical and defend your answer.
5. Determine the upstream and downstream Froude numbers.

Solution:

The diagram of the flow is depicted below, as well as the corresponding E-y diagram. The specific discharge for a channel of 10 ft is calculated below:

$q_{1}={\frac {Q}{w_{1}}}={\frac {150}{10.0}}=15.0{\text{ ft}}^{2}/s$

This corresponds to the blue curve on the e-y diagram. The specific discharge for a channel of 5 ft is calculated as:

$q_{2}={\frac {Q}{w_{2}}}={\frac {150}{5.00}}=30.0{\text{ ft}}^{2}/s$

This specific discharge corresponds to the red curve on the E-y diagram.

A diagram of the channel is depicted below:

The E-y diagram of the simultaneous step and constriction is presented below: E-y diagram of channel encountering a constriction and downwards step

Step1: Determine the minimum width that can pass the current flow. The minimum width where a choke does not happen occurs at critical conditions downstream. A downwards step acts as an “energy gift” and therefore increases energy downstream of the flow.

$E_{2}=E_{1}+Z$ $E_{2}=4.00+2.00=6.00{\text{ ft}}$ $E_{2}=E_{c}=6.00{\text{ ft}}$ $y_{2c}={\frac {2}{3}}\times E_{2}c={\frac {2}{3}}\times 6.00=4.00{\text{ ft}}$ $y_{2c}=\left({\frac {q_{\mathrm {max} }^{2}}{g}}\right)^{\frac {1}{3}}$ $4.00=\left({\frac {q_{\mathrm {max} }^{2}}{32.2}}\right)^{\frac {1}{3}}$ $q_{max}=45.4{\text{ ft}}^{2}/s$ $w_{min}={\frac {Q}{q_{max}}}={\frac {150}{45.5}}=3.30{\text{ ft}}$

Step 2:Determine if the current conditions cause a choked flow.

$w_{2}=5.0{\text{ ft and }}w_{m}in=3.30{\text{ ft}}$

w_2 is greater than w_{min} and therefore no choke occurs.

Step 3:Determine the energy downstream, E_2.

$E_{2}=E_{1}+Z$ $E_{2}=4.00+2.00=6.00{\text{ ft}}$

Step 4:What is the depth downstream with current conditions (w_2 = 5.00 ft)?

$q_{2}=30.0{\text{ ft}}^{2}/s$ $E_{2}=y_{2}+{\frac {q_{2}^{2}}{2gy_{2}^{2}}}$ $6.00=y_{2}+{\frac {30.0^{2}}{2(32.2)y_{2}^{2}}}$ $y_{2}=5.55{\text{ ft}}$ The other root, which is a supercritical depth is 1.83 ft.

Step 5:Determine if y_2 is subcritical or supercritical and defend your answer.

The equation in Step 4 yields two alternate depths but the correct depth downstream is subcritical because only the subcritical root is accessible. The downwards step adds energy to the flow and the constriction increases the specific discharge which corresponds to an increase in flow depth. This can be seen in the following E-y diagram:

E-y diagram of channel encountering a constriction and downwards step without a choke

Step 6:Determine the Froude numbers upstream and downstream.

$Fr={\frac {q}{y\times {\sqrt {gy}}}}$ $Fr_{1}={\frac {15}{3.75\times {\sqrt {(32.2)(3.75)}}}}=0.36$ $Fr_{2}={\frac {30}{5.55\times {\sqrt {(32.2)(5.55)}}}}=0.40$

PART B

A choke occurs where the width downstream is 3.00 ft, but the flowrate into the system remains the same. With these new flow conditions:

1. Determine the start of transient downstream depth.
2. Determine the start of transient downstream specific discharge.
3. Determine the steady state downstream depth.
4. Determine the steady state downstream energy.
5. Determine the steady state upstream energy.
6. Determine the steady state upstream depth.

Solution:

Step1: Determine the start of transient downstream depth.

The start of transient downstream depth occurs as a critical depth where the corresponding start of transient downstream energy is critical.

$E_{2}=E_{1}+Z$ $E_{2}=4.00+2.00=6.00{\text{ ft}}$ $E_{2}=E_{trans,c}=6.00{\text{ ft}}$ $y_{2trans,c}={\frac {2}{3}}\times E_{2}c={\frac {2}{3}}\times 6.00=4.00{\text{ ft}}$

Step 2:Determine the start of transient downstream specific discharge.

$y_{2trans}=\left({\frac {q_{\mathrm {trans} }^{2}}{g}}\right)^{\frac {1}{3}}$ $4.00=\left({\frac {q_{\mathrm {trans} }^{2}}{32.2}}\right)^{\frac {1}{3}}$ $q_{trans}=45.4{\text{ ft}}^{2}/s$

Step 3:Determine the steady state downstream depth.

$q_{2}={\frac {Q}{w_{2}}}={\frac {150}{3}}=30{\text{ ft}}^{2}/s$ $y_{2ss}=y_{c}$ $y_{2ss}=\left({\frac {q_{2}^{2}}{g}}\right)^{\frac {1}{3}}=\left({\frac {50.0^{2}}{32.2}}\right)^{\frac {1}{3}}=4.27{\text{ ft}}$

Step 4:Determine the steady state downstream energy.

$E_{2ss}=E_{c}$ $E_{2ss}={\frac {3}{2}}\times y_{2ss}={\frac {3}{2}}\times 4.27=6.40{\text{ ft}}$

Step 5:Determine the new upstream steady state energy.

$E_{2ss}=E_{1ss}+Z$ $E_{1ss}=E_{2ss}-Z=6.40-2.00=4.40{\text{ ft}}$

Step 6:Determine the new steady state upstream depth.

$E_{1ss}=y_{1ss}+{\frac {q_{1}^{2}}{2gy_{1ss}^{2}}}$ $4.40=y_{1ss}+{\frac {15.0^{2}}{2(32.2)y_{1ss}^{2}}}$ $y_{1ss}=4.20{\text{ ft}}$

The E-y diagram with the transient depths, transient energies, transient specific discharge, steady state depths, and steady state energies is provided below. The black lines point to the transient measurements while the red lines point to the steady state measurements.

E-y diagram of channel encountering a constriction and downwards step with a choke

E_{1trans} is 4.00 ft with a depth, y_{1trans}, of 3.75 ft. E_{2trans} is 6.00 ft with a depth, y_{2,trans}, of 4.00 ft. E_{1ss} is 4.40 ft with a depth, y_{1ss}, of 4.20 ft. E_{2ss} is 6.40  ft with a depth, y_{2ss}, of 4.27 ft.

PART C

If the same choke is presented and the height of the step can be adjusted, what is the minimum downward step that is needed in order to avoid a choke and keep the same initial upstream flow conditions as initially specified.

$y_{2}=y_{c}$ $y_{2c}=\left({\frac {q_{2}^{2}}{g}}\right)^{\frac {1}{3}}=\left({\frac {50.0^{2}}{32.2}}\right)^{\frac {1}{3}}=4.27{\text{ ft}}$ $E_{2}=E_{c}$ $E_{2c}={\frac {3}{2}}\times y_{2c}={\frac {3}{2}}\times 4.27=6.40{\text{ ft}}$ $Z_{min}=E_{2c}-E_{1}=6.40-4.00=2.40{\text{ ft}}$

E-y diagram of channel encountering a constriction and downwards step with minimum step to avoid a choke

Transient flow at a choke in a rectangular channel

When a choke is present, the amount of energy in the flow upstream of the choke is insufficient to maintain the flow rate downstream; therefore, a choke would cause a reduction in flow rate moving through the constriction (obstruction) at the section causing the choke. This reduced flow rate is known as the transient flow rate. The transient flow rate is lesser in magnitude compared with the flow rate upstream of the choke, also known as the steady state flow rate.

Since the flow rate through the choke section is reduced, some volume of water is being prevented from passing through the choke section causing water to accumulate just upstream of the choke. When water starts accumulating, the storage volume, the depth of flow, and the energy associated with this depth increases. Hence, over time, enough water will accumulate upstream of the constriction (obstruction) such that the choke can be overcome through the resulting increase in energy enabling the flow upstream to pass the obstruction without flow reduction. During this process of energy build up, the transient flow will approach the steady state flow rate over some period of time. The time that the flow takes to overcome the choke is dependent on the storage conditions upstream of the choke.

A choke can happen at various flow transition points in an open channel flow. This discussion below presents the case for a choke at an energy conserving sluice gate in a rectangular channel.

Choke flow at a smooth sluice gate

To appreciate the effects of a choke at a sluice gate, it is important to understand the transient conditions from the onset of the choke conditions to the return to the steady state flow rate. To investigate these transient conditions, some comments about the discharge through choke inducing structure, the upstream storage conditions, and flow balance should be made.

Discharge through the sluice gate at a rectangular section

Looking at Figure A, the following Bernoulli’s equation can be presented for a streamline at the upstream (1) and downstream (2)sections of the gate for a horizontal and frictionless channel:

FIGURE A

$E_{1}={\frac {v_{1}^{2}}{2g}}+y_{1}={\frac {v_{2}^{2}}{2g}}+y_{2}=E_{2}$

Considering the specific energy, E, upstream and downstream of the gate for a horizontal channel.

The following equation solves for the velocity downstream of the gate:

$v_{2}={\sqrt {2g{\bigl (}E_{1}-y_{2}{\bigr )}}}$

Flowrate per unit width at the gate, q_g, is given by:

$q_{2}=y_{2}\cdot {\sqrt {2g{\bigl (}E_{1}-y_{2}{\bigr )}}}=q_{g}=y_{g}\cdot {\sqrt {2g\cdot h}}$

Where:

${\text{h}}=E_{1}-y_{2}$

The flow rate per unit width downstream is the same as the flow rate at the gate because, for an energy conserving sluice gate, the flow depths downstream of the gate and at the gate are the same rendering the velocity and cross-sectional area the same as well. The equation above for q_g is similar to the rectangular orifice discharge equation for flow per unit width with the coefficient of discharge set equal to unity. This equation allows for solving for the flow at the gate with every incremental change in energy upstream.

Stage-storage relationship upstream of the sluice gate

The storage characteristics upstream of the sluice gate, along with the continuity equation, will determine how long each incremental transient flow increase takes. This stage-storage relationship is different from stage – discharge relationship (also known as the rating curve).For the simplicity of our consideration, the channel is a rectangular channel of length, L, and a unit width, W, as seen in Figure A above. The storage, S, upstream of the gate can be related to depth, y, in the following equation for a rectangular channel:

$S=LWy$

The third and final consideration for the investigation of transient conditions is flow balance in the channel performed using the continuity equation.

Continuity equation

Based on the continuity equation, for a rectangular channel with a unit width, W, it can be said that

$\left({\frac {\Delta S}{\Delta t}}\right)_{i}=I-O=q^{ss}-q_{i}^{trans}$

Where:	I = Inflow to the gate (length3/time)		O = Outflow through the gate (length3/time)
	qitrans = transient unit discharge at the gate at time step i(length2/time)		qss = steady state unit discharge upstream of gate(length2/time)
	$\Delta S_{i}$ = $S_{i}-S_{i-1}$ change in storage (length3)		$\Delta t_{i}$ = $t_{i}-t_{i-1}$ incremental time (time)
	i = indicates the time step

Example Problem

Consider the scenario for a sluice gate located in a rectangular channel with dimensions as shown in Figure A of length, L=2000.0 ft. and width, W= 1.0 ft. The flow before a sluice gate produces a choke is, q_ss= 10.0 ft^2/s. and the depth upstream before the choke, y₁^upstream=3.5 ft. with the specific energy, E_int.=3.63 ft.

Figure A. A sluice gate placed in a rectangular open channel. The channel is 1 ft. wide and is 2000 ft. long upstream of the gate.

Figure B. The increase in storage upstream with time to overcome choke.

Figure C. Change of flowrate through the gate from the onset of the choke to steady state conditions (t=19.8 hr).

Figure D. The stage-discharge curve showing relationship between flow depth upstream of the gate and discharge through the gate.

Solving for initial and steady state conditions

If the gate is lowered anywhere below the alternate depth to the upstream flow depth (y_alternate=y_g=0.73 ft.), then a choke is produced. Therefore, for a sluice gate lowered to a depth of y_g=0.5 ft, produce the results for
Part 1) The steady state energy upstream of the gate, E_ss,us,
Part 2) The steady state depth upstream of the gate,y_ss,us,
Part 3) The initial flow through gate the instant the gate is lowered to a depth of 0.5 ft.,q_int,g,
Part 4) The initial storage before the choke is introduced, S_int,
Part 5) The total storage required for overcoming the choke S_ss.

Solution:

Part 1) E_ss,us, steady state energy upstream of the gate can be determined by recognizing that it is equal to energy at the gate:

$E_{ss,us}=y_{g}+{\frac {q_{ss}^{2}}{2gy_{g}^{2}}}=0.5+{\frac {10.0^{2}}{2(32.2)0.5^{2}}}=6.71{\text{ ft}}$

Part 2) Steady state depth upstream of gate, y_ss,us, is given by the alternate depth equation equation evaluated using steady state flowrate:

$y_{ss,us}={\frac {2y_{g}}{-1+{\sqrt {1+{\frac {8gy_{g}^{3}}{q_{ss}^{2}}}}}}}={\frac {(2)(0.5)}{-1+{\sqrt {1+{\frac {8(32.2)(0.5)^{3}}{10^{2}}}}}}}=6.68{\text{ ft}}$

Part 3) Initial flow through the gate, q_int,g, is given by the evaluating the discharge through the gate as discussed above. The energy considered here is the specific energy upstream of the gate at the instant a choke is produced.

$q_{int,g}=y_{g}\cdot {\sqrt {2g{\bigl (}E_{int,us}-y_{g}{\bigr )}}}=0.5\cdot {\sqrt {2\times 32.2\times \left(3.63-0.5\right)}}=7.1{\text{ ft}}^{2}/{\text{s}}$

Part 4)The storage upstream of the gate prior to the onset of the choke, S_int, is given by

$S_{int}=LWy_{int,us}=2000.0ft.\cdot 1ft.\cdot 3.5ft.=7000ft^{3}$

Part 5)The storage upstream of the gate after having overcome the choke, S_ss, is given by

$S_{ss}=LWy_{ss,us}=2000.0ft.\cdot 1ft.\cdot 6.68ft.=13,353ft^{3}$

Solving for transient conditions during the first time step, Δt_{i = 1}

For the same sluice gate choke conditions mentioned above, produce the results for
Part 6)The change in flow rate ∆S/∆t_i=1 between flow upstream of the gate (inflow) and flow leaving the gate (outflow) during the first time step
Part 7)The new flow depth upstream of the gate after the time increment ∆t _i=1
Part 8)The associated change in storage, ∆S _i=1
Part 9)The time increment (∆t) for the change in storage specified in the first time step

Solution:
Part 6)In a 1 ft. wide rectangular channel, the change in flow rate ∆S/∆t _i=1 is determined by applying the continuity equation:

$\left({\frac {\Delta S}{\Delta t}}\right)_{i=1}=I-O=q^{ss}-q_{i=1}^{trans}=10.0{\text{ ft}}^{3}/{\text{s}}-7.1{\text{ ft}}^{3}/{\text{s}}=2.9{\text{ ft}}^{3}/{\text{s}}$

Part 7)The flow depth upstream of the gate at the end of the first time step, ∆t _i=1 is given by applying the alternate depth equation with unit discharge taken at the beginning of the time step:

$y_{i=1,us}={\frac {2y_{g}}{-1+{\sqrt {1+{\frac {8gy_{g}^{3}}{q_{i=1}^{2}}}}}}}={\frac {(2)(0.50)}{-1+{\sqrt {1+{\frac {8(32.2)(0.50)^{3}}{7.10^{2}}}}}}}=3.57{\text{ ft}}$

Part 8)The associated change in storage, ∆S _i=1
, is

$\Delta S_{i=1}=S_{i=1}-S_{i-1}={\big (}2000.0{\text{ ft}}\cdot 1{\text{ ft}}\cdot 3.57{\text{ ft}}{\big )}-7000{\text{ ft}}^{3}=130.5{\text{ ft}}^{3}$

Part 9)The time increment (∆t) _i=1 can then be given by

$\Delta t_{i=1}={\frac {\Delta S_{i=1}}{\left({\frac {\Delta S}{\Delta t}}\right)_{i=1}}}={\frac {130.5{\text{ ft}}^{3}}{2.9{\text{ ft}}^{3}/{\text{ s}}}}=44.9{\text{ s}}$

Elapsed time after the second time step t_{i = 2} = Δt_{i = 2} + Δt_{i = 1}

One can find the total time that has elapsed with adding each of time steps. Therefore, at the total time at the end of the second time step is the sum of the first two time steps. By the same logic, with an estimate of each time increment associated with every change in transient flow rate until the time of steady state conditions at the gate, one can determine the total time required to overcome the choke.

For finding the total time after the second time increment, one needs to answer the following questions:
Part 10) What is the new specific energy for the flow upstream of the gate?
Part 11) What is the transient flow through the gate at the end of the second time step?
Part 12) What is the new change in flow rate between the flow upstream and through the gate?
Part 13) What is the new flow depth at the end of the second time step?
Part 14) What is the associated change in storage from the previous time step?
Part 15) What is the time increment for the second time step?
Part 16) What is the total time at the end of the second time step?

Solution:
Part 10) To find the new specific energy for the upstream flow depth during the second time step, it is important to recognize that the constriction doesn’t affect the flow rate upstream. Therefore, for the same flow upstream as in time step 1, the flow depth has increased at the end of the first time step. Specific energy upstream of the gate at the beginning of the second time step, E_i=2,us, is given by the specific energy equation considering the flow depth upstream at the end of the first time step:

$E_{i=2,us}=y_{i=1,us}+{\frac {q_{ss,us}^{2}}{2gy_{i=1,us}^{2}}}=3.57+{\frac {10.0^{2}}{2(32.2)3.57^{2}}}=3.69{\text{ ft}}$

Part 11) To find transient flow through the gate from the end of the first time step to the end of the second time step,q_2,g one would need to find the discharge through the gate after the increase in flow depth upstream:

$q_{i=2,g}=y_{g}\cdot {\sqrt {2g{\bigl (}E_{i=2,us}-y_{g}{\bigr )}}}=0.5\cdot {\sqrt {2\cdot 32.2\cdot \left(3.69-0.5\right)}}=7.16{\text{ ft}}^{2}/{\text{s}}$

Part 12) The change in flow rate at the end of the second time step, ∆S/∆t _i=2, is given by applying continuity:

$\left({\frac {\Delta S}{\Delta t}}\right)_{i=2}=I-O=q^{ss}-q_{i=2}^{trans}=10.0{\text{ ft}}^{3}/{\text{s}}-7.16{\text{ ft}}^{3}/{\text{s}}=2.84{\text{ ft}}^{3}/{\text{s}}$

Part 13) The flow depth at the end of the second time step upstream of the gate is given by the alternate depth equation using unit discharge found in Part 11:

$y_{i=2,us}={\frac {2y_{g}}{-1+{\sqrt {1+{\frac {8gy_{g}^{3}}{q_{i=2}^{2}}}}}}}={\frac {(2)(0.5)}{-1+{\sqrt {1+{\frac {8(32.2)(0.50)^{3}}{7.16^{2}}}}}}}=3.63{\text{ ft}}$

Part 14) The associated change in storage from the first to the second time step is given by

$\Delta S_{i=1}=S_{i=2}-S_{i-1}={\big (}2000.0{\text{ ft}}\cdot 1{\text{ ft}}\cdot 3.63{\text{ ft}}{\big )}-7130.5{\text{ ft}}^{3}=123.2{\text{ ft}}^{3}$

Part 15) The second time step increment can then be given by

$\Delta t_{i=2}={\frac {\Delta S_{i=2}}{\left({\frac {\Delta S}{\Delta t}}\right)_{i=2}}}={\frac {123.2{\text{ ft}}^{3}}{2.84{\text{ ft}}^{3}/{\text{ s}}}}=43.4{\text{ s}}$

Part 16) In finding the total time required for the completion of the first two time steps, one would just sum all time increments

$t_{i=2}=\Delta t_{i=2}+\Delta t_{i=1}=43.4{\text{ s}}+44.9{\text{ s}}=88.3{\text{ s}}$

Thus, after 88.3 s since the choke was introduced the flow has increased from 7.10 ft³/s to 7.16 ft³/s. Moreover, as a result of the increase in storage upstream of the gate, the energy has increased from 3.63 ft. to 3.69 ft.

General comments about the transition from choke flow

Calculating the flow characteristics at every time increment allows one to study the transient flow conditions; this was the aim of the discussion above.

• After numerous time steps, the depth upstream will increase to steady state depth, y_ss=6.68 ft. and an associated steady state specific energy, E_ss= 6.71 ft. However, for this to happen, the channel upstream of the gate has to increase in volume by 6353 ft³ from 7000 ft³. The change in storage with respect to time is presented in Figure B after having calculated the flow characteristics at numerous time steps.

• Flowrate instantaneously gets reduced at the onset of a choke from 10 ft³/s to 7.10 ft³/s. As can be seen in Figure C, after this instantaneous reduction in flowrate, it steadily increases eventually reaching steady state discharge of 10 ft³/s. The time that it takes to get back to steady state discharge for this example problem was calculated to be 19.8 hours.

• The Stage discharge relationship is presented in Figure D. The figure shows how the discharge through the gate increases with increasing flow depth upstream of the gate. The precipitous drop in flowrate in the figure corresponds to the time the choke is imposed reducing the discharge from a value of 10 ft³/s to just over 7 ft³/s. When depth upstream gets to a value just under 6.7 ft., the choke of flow through the gate has been overcome, and the stage upstream need not increase because steady state discharge and energy has been achieved.

References

1. M. H. Chaudhry, Open-Channel Flow. New York: Springer, 2008.
2. K. Subramanya, Flow in open channel.Tata McGraw-Hill Education, Nov 1, 2001
3. Moglen, G.E. (2011) Lecture notes from CEE 4324/5984: Open Channel Flow, Virginia Tech <http://filebox.vt.edu/users/moglen/ocf/index.html>
4. Henderson, F.M., 1966. Open Channel Flow, Prentice-Hall.
5. Ven Te Chow, Open-Channel Hydraulics,New York, 1959, McGraw-Hill.
6. Das Madan Mohan, Open Channel Flow, Phi Learning, 2008
7. http://ocw.mit.edu/courses/earth-atmospheric-and-planetary-sciences/12-090-special-topics-an-introduction-to-fluid-motions-sediment-transport-and-current-generated-sedimentary-structures-fall-2006/lecture-notes/ch5.pdf
8. http://udel.edu/~inamdar/EGTE215/Open_channel.pdf
9. http://streams.osu.edu/book/equation_pdf/Ch8-Equations.pdf