CAGD/Bézier Curves
Bézier curves are very common in the field of CAGD. They were invented by Dr. Pierre Bézier, an engineer for the Renault automotive company. The goal was to create an intuitive method to allow designers and engineers to create curves. Since construction of curves and shapes from purely mathematical equations can be a daunting task, Bézier curves allow shape generation to be a rather simple task. More information on them can be found on the Wikipedia page.
Definition
[edit | edit source]
A Bézier curve is a parametric curve. It depends on certain control points that often mimic the shape of the resulting curve. In the example at left, they are the labeled points. The shape of the resulting curve is determined by blending functions. Blending functions are functions of the parameter of the curve and depending on their equations, they can change the shape of the curve.
A standard n-degree Bézier curve is defined as follows:
The value of each point on the curve depends on the sum of the blending functions multiplied by the control point values. In this equation, the blending functions are denoted B(t). Everything is fairly self-explanatory except the term . This is commonly known as the binomial coefficient. It arises from a binomial expansion and is related to Pascal's triangle. A mathematical definition for this term is:
This definition isn't very helpful in computing algorithms because of the recursive nature of the factorial. The recurrence relationship solves this problem:
Since we know that the binomial coefficient is 1 when i=0, we can just multiply the fractional term with every iteration of i. In a CAD system with multiple Bézier curves, this cuts down computation time significantly. For the standard Bézier curve, the domain for the parameter t is [0,1].
Relationship to Bernstein polynomials
[edit | edit source]A Bézier curve can be written as a set of n Bernstein polynomials, where n is the dimension of the Bézier curve. A Bernstein polynomial B(t) has the standard form:
A 3D Bézier curve P(t) can be expressed thus:
Arbitrary Parameter Intervals
[edit | edit source]The domain for a standard parameter t is [0,1]. However, Bézier curves can be defined for any range of parameters. The conditions of the interval should be such that:
The de Casteljau Algorithm
[edit | edit source]
The de Casteljau algorithm is a way to subdivide a Bézier curve into 2 separate curves. It was developed by Paul de Casteljau, an engineer who worked for the Citroën automobile company. If a curve has a parameter interval from , then the algorithm would yield 2 curves with a common parameter so that one curve has an interval from and the other has one from
In order to facilitate the algorithm, we define the control points with a superscript, The original control points correspond to j=0. The algorithm is defined as follows:
- ,
where j is the iteration of the computation. We will construct a computation table where j is the iteration of the computation. The computation table in general will look like this:
We now have the control points for the respective curves. One curve contains the control points , which are the points in the leftmost column, and the other curve contains the control points , which are the points on the diagonal of the table above.
The de Casteljau algorithm has T(n) =O(n2) time complexity. It is very numerically stable, however.
Degree Elevation of Bézier Curves
[edit | edit source]It can be shown that any n-degree Bézier curve can be expressed by another Bézier curve of degree n+1. There are two main identities that we must have in order to show this:
These identities can be derived from the Bézier curve definition. The proof starts by multiplying the Bézier curve by [(1-t)+t]:
Thus we have the following relationship between the control points:
If the degree elevation is performed repeatedly so that the degree of the curve approaches infinity, the control polygon converges to the curve itself.
Derivatives of Bézier Curves
[edit | edit source]Bézier curves with degree n have parametric derivatives that can be expressed as Bézier curves of degree n-1. If a Bézier curve has an arbitrary interval [t0,t1], then the control points of the derivative can be expressed as:
A generalization of the derivative equation is:
The curve of the first derivative of a standard Bézier curve is known as a hodograph. If the curve passes through the origin of the hodograph, it corresponds to a cusp on the original curve. This notion of a derivative doesn't extend to rational Bézier curves. It only applies to standard ones. Rational Bézier curves have derivatives that involve the quotient rule, so this formula doesn't apply. Consequently, rational Bézier curves of degree n have derivatives that can be expressed as a rational Bézier curve of degree 2n.
3D Bézier Curves
[edit | edit source]Bézier curves can be defined in three dimensions. The de Casteljau algorithm, degree elevation, and hodographs extend into 3D space. This will prove very useful when discussing rational Bézier curves.
Rational Bézier Curves
[edit | edit source]Sometimes we want more control and versatility in our Bézier curves. We can assign a scalar weight to each control point in order to make the curve more versatile. If we divide by the sum of the scalar weights and blending functions, we get a rational Bézier curve:
The blending functions are rational polynomials, or the ratio of two polynomials. If the weights of the control points are all 1, the rational Bézier reduces to a standard polynomial Bézier curve. Rational Bézier curves are useful for lots of reasons. A degree 2 polynomial Bézier curve can only represent a parabola. An exact representation of a circle requires a degree 2 rational Bézier curve. As well, a perspective drawing of a polynomial 3D Bézier curve is a rational Bézier curve. If we define a point in 3D space as , we get a kind of cone where the point of the cone is at the origin and the base is the 3D curve. This would contain all the lines that extend from the point of the cone to a point on the curve. Each point in 3D space maps to a corresponding point in 2D space . Thus, the point corresponds to a 2D point on the z=1 plane.
This cone paradigm helps us when we try to implement the de Casteljau or degree elevation algorithms on rational Bézier curves. In order to use these algorithms, we first need to convert the 2D rational Bézier to a 3D polynomial curve. Then, implement the algorithm. Afterward, convert the result back into a 2D rational curve. Again, derivatives can't be implemented like above. To calculate the derivative, the rational Bézier curve needs to be split into its respective coordinates:
From calculus, we can implement the quotient rule:
The math gets simpler by only evaluating the derivative at the endpoints. Thus, we get the following relationships for a Bézier curve over any arbitrary interval :
Curvature of a Bézier Curve
[edit | edit source]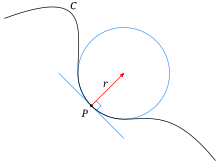
Curvature for a curve at a certain point is defined as the reciprocal of the radius of the osculating circle. In the figure at left, the osculating circle is marked in blue for curve C at point P. At P, the tangent lines for the curve and the circle are equal. The radius of the osculating circle is called the radius of curvature. The curvature is then the reciprocal of that radius. A straight line has a curvature of zero, but has an infinite radius of curvature.
A parametric curve has a fairly complex equation for curvature:
This equation simplifies dramatically when evaluated at the endpoint of a Bézier curve:
In this equation, c is simply the distance between the endpoint and the second control point (P0 and P1) and d is the perpendicular distance from the third control point (P2) and the line formed by the first and second control points. Since Bézier curves are symmetrical, this can be used at either endpoint of the curve.
It is very common to want to know the curvature at point between the endpoints. This formula doesn't seem that useful, despite its elegance. However, a very clever trick can be employed to use this equation. Any Bézier curve can be split into two curves at the desired point using the de Casteljau algorithm and this formula can be employed at the endpoint of either of the resulting curves.
Continuity of Bézier Curves
[edit | edit source]Continuity refers to the smoothness of the derivatives of a curve. There are really two different types of continuity that are important in CAGD: parametric and geometric. The symbols we use to represent nth order continuity are Cn or Gn, respectively. In general, curves that are Gn can be reparameterized so that the curves are Cn. In addition, curves that are Cn are also Gn if the equations for Cn hold and if the first n derivatives of either curve are not zero.
Parametric Continuity
[edit | edit source]Parametric continuity between two curves constrains not only the magnitude of the derivative, but also the parameter values for each curve. Two curves P[t0, t1] and Q[t1, t2] have nth order parametric continuity (are Cn) if:
In the case above, t1 is the point where P and Q are joined. C0 then means only that the endpoints are coincident. C1 means that the endpoints are coincident and that the tangent of both curves has the same magnitude and direction at the same parameter value. C2 means that the curves are C1 and C0 as well as the curvature having the same magnitude and direction for both curves.
Geometric Continuity
[edit | edit source]Geometric continuity can be viewed as a less strict way of constraining two curves. Geometric continuity is also known as visual continuity. Unlike with parametric continuity, the values of the derivatives aren't bound to specific parameter values. This means that two curves that are G0 are coincident, but they do not need to have the same parameter value at that point, that is, P(1) doesn't need to equal Q(1). Further, two curves that are G1 are G0 and in addition must have a common tangent line, but the magnitudes of the tangent vectors don't have to be the same. Curves that are G2 are G0 and G1 and have the same center of curvature at the point that they are joined.
Reparameterization of Bézier Curves
[edit | edit source]A reparameterization of a curve is simply changing the values of the curve to correspond to a different parameter value. For any parametric curve Q(t), we can substitute another parameter s in for the parameter t that has a relationship to t (for example, s = 2t + 3). This would yield a new curve R(s). If the domains for the curves are infinite, the new curve would be geometrically identical since they are made up of the same points. Thus, we can say that Q(t) = R(s). We have changed the parameterization of the curve without changing any of the control points. Just as we would expect with any new parameterization, Q(0.5) is not equal to R(0.5).
If we have intervals on our curves, as in Bézier curves, then a simple reparameterization technique would be just to make an equation relating a new parameter to the old one, as in the above example. For the curve P[t0,t1](t) and the reparameterized curve Q[s0,s1](s), they would have the same degree, the same control points and the same weights, however, the interval for Q(s) would not be the same as for P(t), or in other words, t0 ≠ s0 and t1 ≠ s1. If the new interval is known, then the reparametrization can be expressed as .
A rational Bézier curve can be reparameterized by using a similar substitution: . Because of this special substitution, it's possible to reparameterize the curve without changing the endpoints of the curve segment, or in other words, not changing the interval. This special substitution takes the form , where u is the new parameter and the variables a,b,c,d are simply constants we must determine. For most cases, 0 ≤ t ≤ 1, so we would want 0 ≤ u ≤ 1 as well. If t = 0 when u = 0, then a = 0. If t = 1 when u = 1, then c = 1 and d = b. This yields the new substitutions:
A general rational Bézier curve is described with the following equation:
Using our substitutions and multiplying numerator and denominator by and simplifying, we get the following:
This proves that we can reparameterize a rational Bézier curve by simply multiplying the weights by bi, something very simple. The constant b can be chosen to be anything, since there are no restrictions placed on it from the parametrization. This kind of reparameterization is often useful in graphics, because a rational Bézier curve will look smoother if its weight ratio is minimized. The weight ratio is the ratio of the largest weight of the curve to the smallest weight. For example, a curve with weights 8,2,3,1 (weight ratio = 8) won't look as smooth as the curve 2,1,3,2 (weight ratio = 2).
Explicit Bézier Curves
[edit | edit source]A special case of parametric curves is when we define the parameterization x=t. This is called an explicit Bézier curve. For polynomial Bézier curves, when this parametrization is defined, the x-coordinates of the control points are evenly spaced over the interval where the curve is defined. The curve is really just a Bernstein polynomial. There are many advantages to explicit Bézier curves and we will discuss them when these advantages arise.







![{\displaystyle \mathbf {P} _{[t_{0},t_{1}]}(t)={\frac {\sum _{i=0}^{n}{\tbinom {n}{i}}(t_{1}-t)^{n-i}(t-t_{0})^{i}\mathbf {P} _{i}}{(t_{1}-t_{0})^{n}}}=\sum _{i=0}^{n}{\binom {n}{i}}\left({\frac {t_{1}-t}{t_{1}-t_{0}}}\right)^{n-i}\left({\frac {t-t_{0}}{t_{1}-t_{0}}}\right)^{i}\mathbf {P} _{i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9201b936286051662464ffea30e0c70f69257421)
![{\displaystyle [t_{0},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/639e60bd8940fb661014a51c7ff1e8e257dc3206)
![{\displaystyle t_{1}\in [t_{0},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2af920c7030cf63024bcd8fdee411441c6840d4e)
![{\displaystyle [t_{0},t_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)
![{\displaystyle [t_{1},t_{2}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a4af0fbfdd3345230f249cecd51addfdb51e1c4)







![{\displaystyle {\begin{aligned}\mathbf {P} (t)&=[(1-t)+t]\mathbf {P} (t)\\&=[(1-t)+t]\sum _{i=0}^{n}\mathbf {P} _{i}B_{i}^{n}(t)\\&=\sum _{i=0}^{n}\mathbf {P} _{i}[(1-t)B_{i}^{n}(t)+tB_{i}^{n}(t)]\\&=\sum _{i=0}^{n}\mathbf {P} _{i}\left[{\frac {n+1-i}{n+1}}B_{i}^{n+1}(t)+{\frac {i+1}{n+1}}B_{i+1}^{n+1}(t)\right]\\&=\sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {P} _{i}B_{i}^{n+1}(t)+\sum _{i=0}^{n}{\frac {i+1}{n+1}}\mathbf {P} _{i}B_{i+1}^{n+1}(t)\\&=\sum _{i=0}^{n}{\frac {n+1-i}{n+1}}\mathbf {P} _{i}B_{i}^{n+1}(t)+\sum _{i=1}^{n+1}{\frac {i}{n+1}}\mathbf {P} _{i-1}B_{i}^{n+1}(t)\\&=\sum _{i=0}^{n+1}{\frac {n+1-i}{n+1}}\mathbf {P} _{i}B_{i}^{n+1}(t)+\sum _{i=0}^{n+1}{\frac {i}{n+1}}\mathbf {P} _{i-1}B_{i}^{n+1}(t)\\&=\sum _{i=0}^{n+1}\left[{\frac {(n+1-i)\mathbf {P} _{i}+i\mathbf {P} _{i-1}}{n+1}}\right]B_{i}^{n+1}(t)\\&=\sum _{i=0}^{n+1}\mathbf {P} _{i}^{*}B_{i}^{n+1}(t)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a89917d8b65ecbd02835d9f8f5f3cd2d6ad540a6)










![{\displaystyle \mathbf {P} _{[t_{0},t_{1}]}(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ccd5a7e18b74395d1db442f8821ab2b1d7fd875)










