Three stress measures are widely used in continuum mechanics (particularly in the computational context). These are
The Cauchy stress (
σ
{\displaystyle {\boldsymbol {\sigma }}}
The Nominal stress (
N
{\displaystyle {\boldsymbol {N}}}
P
=
N
T
{\displaystyle {\boldsymbol {P}}={\boldsymbol {N}}^{T}}
The second Piola-Kirchhoff stress or PK2 stress (
S
{\displaystyle {\boldsymbol {S}}}
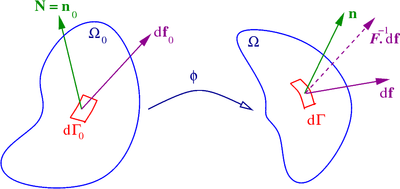
Consider the situation shown the following figure.
Quantities used in the definition of stress measures
The following definitions use the information in the figure. In the reference configuration
Ω
0
{\displaystyle \Omega _{0}}
d
Γ
0
{\displaystyle d\Gamma _{0}}
N
≡
n
0
{\displaystyle \mathbf {N} \equiv \mathbf {n} _{0}}
t
0
{\displaystyle \mathbf {t} _{0}}
d
f
0
{\displaystyle d\mathbf {f} _{0}}
Ω
{\displaystyle \Omega }
d
Γ
{\displaystyle d\Gamma }
n
{\displaystyle \mathbf {n} }
t
{\displaystyle \mathbf {t} }
d
f
{\displaystyle d\mathbf {f} }
The Cauchy stress (or true stress) is a measure of the force acting on an element of area in the deformed configuration. This tensor is symmetric and is defined via
d
f
=
t
d
Γ
=
σ
T
⋅
n
d
Γ
{\displaystyle d\mathbf {f} =\mathbf {t} ~d\Gamma ={\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} ~d\Gamma }
or
t
=
σ
T
⋅
n
{\displaystyle \mathbf {t} ={\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} }
where
t
{\displaystyle \mathbf {t} }
n
{\displaystyle \mathbf {n} }
The nominal stress (
N
=
P
T
{\displaystyle {\boldsymbol {N}}={\boldsymbol {P}}^{T}}
P
{\displaystyle {\boldsymbol {P}}}
d
f
=
t
0
d
Γ
0
=
N
T
⋅
n
0
d
Γ
0
=
P
⋅
n
0
d
Γ
0
{\displaystyle d\mathbf {f} =\mathbf {t} _{0}~d\Gamma _{0}={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {P}}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
or
t
0
=
N
T
⋅
n
0
=
P
⋅
n
0
{\displaystyle \mathbf {t} _{0}={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {P}}\cdot \mathbf {n} _{0}}
This stress is unsymmetric and is a two point tensor like the deformation gradient. This is because it relates the force in the deformed configuration to an oriented area vector in the reference configuration.
If we pull back
d
f
{\displaystyle d\mathbf {f} }
d
f
0
=
F
−
1
⋅
d
f
{\displaystyle d\mathbf {f} _{0}={\boldsymbol {F}}^{-1}\cdot d\mathbf {f} }
or,
d
f
0
=
F
−
1
⋅
N
T
⋅
n
0
d
Γ
0
=
F
−
1
⋅
t
0
d
Γ
0
{\displaystyle d\mathbf {f} _{0}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}~d\Gamma _{0}}
The PK2 stress (
S
{\displaystyle {\boldsymbol {S}}}
d
f
0
=
S
T
⋅
n
0
d
Γ
0
=
F
−
1
⋅
t
0
d
Γ
0
{\displaystyle d\mathbf {f} _{0}={\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}~d\Gamma _{0}}
Therefore,
S
T
⋅
n
0
=
F
−
1
⋅
t
0
{\displaystyle {\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {F}}^{-1}\cdot \mathbf {t} _{0}}
Recall Nanson's formula relating areas in the reference and deformed configurations:
n
d
Γ
=
J
F
−
T
⋅
n
0
d
Γ
0
{\displaystyle \mathbf {n} ~d\Gamma =J~{\boldsymbol {F}}^{-T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
Now,
σ
T
⋅
n
d
Γ
=
d
f
=
N
T
⋅
n
0
d
Γ
0
{\displaystyle {\boldsymbol {\sigma }}^{T}\cdot \mathbf {n} ~d\Gamma =d\mathbf {f} ={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
Hence,
σ
T
⋅
(
J
F
−
T
⋅
n
0
d
Γ
0
)
=
N
T
⋅
n
0
d
Γ
0
{\displaystyle {\boldsymbol {\sigma }}^{T}\cdot (J~{\boldsymbol {F}}^{-T}\cdot \mathbf {n} _{0}~d\Gamma _{0})={\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}}
or,
N
T
=
J
(
F
−
1
⋅
σ
)
T
=
J
σ
⋅
F
−
T
{\displaystyle {\boldsymbol {N}}^{T}=J~({\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }})^{T}=J~{\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}}
or,
N
=
J
F
−
1
⋅
σ
and
N
T
=
P
=
J
σ
⋅
F
−
T
{\displaystyle {\boldsymbol {N}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\qquad {\text{and}}\qquad {\boldsymbol {N}}^{T}={\boldsymbol {P}}=J~{\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}}
In index notation,
N
i
j
=
J
F
i
k
−
1
σ
k
j
and
P
i
j
=
J
σ
i
k
F
j
k
−
1
{\displaystyle N_{ij}=J~F_{ik}^{-1}~\sigma _{kj}\qquad {\text{and}}\qquad P_{ij}=J~\sigma _{ik}~F_{jk}^{-1}}
Therefore,
J
σ
=
F
⋅
N
=
P
⋅
F
T
.
{\displaystyle J~{\boldsymbol {\sigma }}={\boldsymbol {F}}\cdot {\boldsymbol {N}}={\boldsymbol {P}}\cdot {\boldsymbol {F}}^{T}~.}
The quantity
τ
=
J
σ
{\displaystyle {\boldsymbol {\tau }}=J~{\boldsymbol {\sigma }}}
Kirchhoff stress tensor and is used widely in numerical algorithms in metal plasticity (where there
is no change in volume during plastic deformation).
Note that
N
{\displaystyle {\boldsymbol {N}}}
P
{\displaystyle {\boldsymbol {P}}}
F
{\displaystyle {\boldsymbol {F}}}
Recall that
N
T
⋅
n
0
d
Γ
0
=
d
f
{\displaystyle {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0}=d\mathbf {f} }
and
d
f
=
F
⋅
d
f
0
=
F
⋅
(
S
T
⋅
n
0
d
Γ
0
)
{\displaystyle d\mathbf {f} ={\boldsymbol {F}}\cdot d\mathbf {f} _{0}={\boldsymbol {F}}\cdot ({\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}~d\Gamma _{0})}
Therefore,
N
T
⋅
n
0
=
F
⋅
S
T
⋅
n
0
{\displaystyle {\boldsymbol {N}}^{T}\cdot \mathbf {n} _{0}={\boldsymbol {F}}\cdot {\boldsymbol {S}}^{T}\cdot \mathbf {n} _{0}}
or (using the symmetry of
S
{\displaystyle {\boldsymbol {S}}}
N
=
S
⋅
F
T
and
P
=
F
⋅
S
{\displaystyle {\boldsymbol {N}}={\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}\qquad {\text{and}}\qquad {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\boldsymbol {S}}}
In index notation,
N
i
j
=
S
i
k
F
j
k
and
P
i
j
=
F
i
k
S
k
j
{\displaystyle N_{ij}=S_{ik}~F_{jk}\qquad {\text{and}}\qquad P_{ij}=F_{ik}~S_{kj}}
Alternatively, we can write
S
=
N
⋅
F
−
T
and
S
=
F
−
1
⋅
P
{\displaystyle {\boldsymbol {S}}={\boldsymbol {N}}\cdot {\boldsymbol {F}}^{-T}\qquad {\text{and}}\qquad {\boldsymbol {S}}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {P}}}
Recall that
N
=
J
F
−
1
⋅
σ
{\displaystyle {\boldsymbol {N}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}}
In terms of the 2nd PK stress, we have
S
⋅
F
T
=
J
F
−
1
⋅
σ
{\displaystyle {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}}
Therefore,
S
=
J
F
−
1
⋅
σ
⋅
F
−
T
=
F
−
1
⋅
τ
⋅
F
−
T
{\displaystyle {\boldsymbol {S}}=J~{\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\sigma }}\cdot {\boldsymbol {F}}^{-T}={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}}
In index notation,
S
i
j
=
F
i
k
−
1
τ
k
l
F
j
l
−
1
{\displaystyle S_{ij}=F_{ik}^{-1}~\tau _{kl}~F_{jl}^{-1}}
Since the Cauchy stress (and hence the Kirchhoff stress) is symmetric, the 2n PK stress is also symmetric.
Alternatively, we can write
σ
=
J
−
1
F
⋅
S
⋅
F
T
{\displaystyle {\boldsymbol {\sigma }}=J^{-1}~{\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}}
or,
τ
=
F
⋅
S
⋅
F
T
.
{\displaystyle {\boldsymbol {\tau }}={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.}
Clearly, from definition of the push-forward and pull-back operations, we have
S
=
φ
∗
[
τ
]
=
F
−
1
⋅
τ
⋅
F
−
T
{\displaystyle {\boldsymbol {S}}=\varphi ^{*}[{\boldsymbol {\tau }}]={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}}
and
τ
=
φ
∗
[
S
]
=
F
⋅
S
⋅
F
T
.
{\displaystyle {\boldsymbol {\tau }}=\varphi _{*}[{\boldsymbol {S}}]={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.}
Therefore,
S
{\displaystyle {\boldsymbol {S}}}
τ
{\displaystyle {\boldsymbol {\tau }}}
F
{\displaystyle {\boldsymbol {F}}}
τ
{\displaystyle {\boldsymbol {\tau }}}
S
{\displaystyle {\boldsymbol {S}}}














































![{\displaystyle {\boldsymbol {S}}=\varphi ^{*}[{\boldsymbol {\tau }}]={\boldsymbol {F}}^{-1}\cdot {\boldsymbol {\tau }}\cdot {\boldsymbol {F}}^{-T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d5f37efb8297f33270efe322adaabf46099ee9)
![{\displaystyle {\boldsymbol {\tau }}=\varphi _{*}[{\boldsymbol {S}}]={\boldsymbol {F}}\cdot {\boldsymbol {S}}\cdot {\boldsymbol {F}}^{T}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3b707f11a8c67a3409dd4df7e6448d0ee9444cb)
