Rindler coordinates(1) are coordinates appropriate for an observer undergoing constant proper acceleration (a constant g-force felt) in an otherwise flat spacetime. Given an unprimed inertial frame set of coordinates, one assigns the accelerated frame observer primed coordinates, "Rindler coordinates", given by


where  is the constant proper acceleration.
is the constant proper acceleration.
First Rindler solved the equation of motion for a constant proper acceleration problem.
If we go to an inertial frame for which a test mass is instantaneously at rest, the four-vector of acceleration will relate to the coordinate acceleration by

, but the length of the four-acceleration is an invariant we're calling the proper acceleration  , so the inertial frame of instantaneous rest coordinate acceleration relates to the proper acceleration by
, so the inertial frame of instantaneous rest coordinate acceleration relates to the proper acceleration by

The coordinate acceleration according to the inertial frame of instantaneous rest relates to the ordinary force by Newton's second law  so we have
so we have

The x component of the ordinary force for a particle of velocity  with respect to the unprimed frame transforms between the two according to
with respect to the unprimed frame transforms between the two according to

And we are considering force along the direction of motion only so


So our equation for proper acceleration becomes

which means that the equation of motion for the case of constant proper acceleration is given by a constant ordinary force constant mass problem given according to whatever inertial frame we use. So we need to solve the equation of motion for a constant ordinary force, constant mass problem.








Integrating and choosing initial conditions so that its initially at zero velocity yields

Using  one can then solve for the time as a function of the proper time
one can then solve for the time as a function of the proper time

and using

one can solve for the position as a function of time

and then the position as a function of proper time

Having both the position and time now as a function of proper time


We merely make a natural choice of primed coordinates for which  is described by those equations of motion. Rindler's choice was
is described by those equations of motion. Rindler's choice was


which does just that.
Rindler's spacetime is then just an accelerated frame transformation of the Minkowski metric of special relativity.
Doing the transformation


transforms the Minkowski line element

into

The Lorentz transformation can be written




If we let  and
and  be functions of the primed time, we can do a transformation given by (2)
be functions of the primed time, we can do a transformation given by (2)




where we are doing anti-derivatives with respect to the primed coordinate time.
It turns out that Rindler's choice of coordinates for an observer undergoing constant proper acceleration is the special case of this transformation where  and
and  are what you would get as a function of the primed time if they were describing constant proper acceleration. Doing this more general transformation for arbitrary time dependent acceleration the line element transforms to
are what you would get as a function of the primed time if they were describing constant proper acceleration. Doing this more general transformation for arbitrary time dependent acceleration the line element transforms to


so for arbitrarily time dependent acceleration, with these transformations you still get the Rindler spacetime, only  is now any function of
is now any function of  instead of a constant.
instead of a constant.
Further, it turns out that for  ,
,  , and
, and  being any three arbitrary functions of
being any three arbitrary functions of  that the line element given by
that the line element given by

Is a zero Riemann tensor exact vacuum solution and so represents a more general accelerated frame transformation of the Minkowski metric of special relativity.
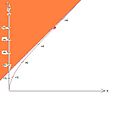
The path of constant proper acceleration as observed by an inertial frame
The red curve of the image shows the path of something undergoing constant proper acceleration with respect to the unprimed inertial frame coordinates which we found was given by

Note it asymptotically approaches the line

The path of a light speed signal lays at 45 degrees. Therefore information from any event in the shaded region will never intersect the path of the accelerated observer so long as he maintains his constant proper acceleration. As such that asymptote constitutes an event horizon from the perspective of the accelerated observer beyond which he can not be reached by any information there. So let's find out where in the accelerated observer's coordinates this asymptote is. Refer to the transformation to Rindler coordinates


First lets move the constant on the second


Next lets replace the  from the equation for the asymptote.
from the equation for the asymptote.


Then square both sides


Now subtract the top equation from the bottom equation

Hyperbolic trig identity

Now the solution to this is

So we see that the event horizon for the accelerated observer is observed by him as a constant distance coordinate behind him.
This time-time element of the contravariant metric tensor in his coordinates is

Note that the event horizon corresponds to a singularity in this element of the metric tensor for his coordinates.
In comparing the physics an observer of constant proper acceleration observes to that a remote observer from an uncharged nonrotating black hole using Schwarzschild coordinates observes, it is best to choose the remote behavior of the accelerated observer's spatial coordinate scaled by the transformation

With this choice of distance coordinate for the accelerated observer, the line element becomes

which is now comperable to the Schwarzschild metric in Schwarzschild coordinates expressed by

(1) Rindler, W., 1969, Essential Relativity: Special, General, and Cosmological, Van Nostrand, New York
(2) Relativity equation 3.3.8