Properties of truth tables

Studies of Boolean functions

Studies of Boolean functions

not dependent on arity: Properties of Boolean functions dependent on arity: Properties of truth tables

The number of Boolean functions with arity $n$ (short for adicity $\leq n$) is $2^{2^{n}}$ ( A001146).

This article is about properties of finite truth tables of Boolean functions, that change with the arity.

simple

• weight: number of true places
• sharpness: weight parity    sharp: odd weight    dull: even weight

subsets

• noble: truth tables that are their own twins
• symmetric: order of inputs does not matter

equivalence classes based on similarity

see also: Extended families and clans of Boolean functions

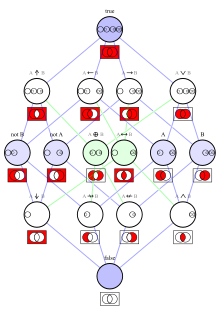
ultra (extension with half-complement)

The two families on the left form a super-family. The family on the right is a super-family on its own. Together these two super-families form an ultra-family.

Each Boolean function has two half-complements. (The truth table is complemented on the left or on the right side.)
A super-family has a unique half-complement. Merging them gives an ultra-family.
As super-clans consist of super-families, they can be extended in the same way.
(Factions do not have a unique half-complement, so it does not seem useful to define ultra-factions.)

ultra-family (negation, complement, half-complement)

The functions in an ultra-family have symmetric positions in a hypercube graph (or the related matrix). See matrices.
This family is a complete ultra-family: 1100 1010     (better seen in its matrix)

ultra-clan (negation, permutation, complement, half-complement)

An ultra-clan is the merge of a super-clan and its half-complement.
It can also be seen as a merge of ultra-families, that are permutations of each other.
See here for a table of the 39 ultra-families of 4-ary Boolean functions.

partitions into blocks of equal size

consul (binary Walsh spectrum)

The Walsh spectrum of a TT is its product with a Walsh matrix.
The binary Walsh spectrum of a TT is its product with a binary Walsh matrix, using F₂ operations (mod 2).
It is always a Walsh function, and shall be called consul. The term is also used for the integer denoting the Walsh function.

The consul integer is the Walsh index of the prefect of the twin. The consul is essentially the prefect of the twin, but without the negation.
(One could also define a sign for the consul, by using a negated binary Walsh matrix. But the sign would just be the sharpness.)

sharp family with consuls 0...7	dull family with consul 2 (compare 4-ary family with consul 6)
3-ary families with Walsh spectra (integers) and consuls (red backgrounds on the right)

tribe

The consul weight is the binary weight of the consul integer. (E.g. consul 6 has consul weight 2.) Dull TT belong to ultra-clans with a unique consul weight, which belong to a dull tribe denoted by that consul weight. Sharp TT form a tribe on their own. 1-ary truth tables Walsh spectra consuls (A253315) tribe 0 1 2 3 [0 0] [1 0] [0 1] [1 1] [ 0 0] [ 1 1] [ 1 -1] [ 2 0] [0 0] [0 0] [0 1] [0 1] 0 0 1 1 0 s s 1 2-ary truth tables Walsh spectra consuls (A253315) tribes sharp: white 0: dark blue 1: light blue 2: green Calculated with this Python script 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 [0 0 0 0] [1 0 0 0] [0 1 0 0] [1 1 0 0] [0 0 1 0] [1 0 1 0] [0 1 1 0] [1 1 1 0] [0 0 0 1] [1 0 0 1] [0 1 0 1] [1 1 0 1] [0 0 1 1] [1 0 1 1] [0 1 1 1] [1 1 1 1] [ 0 0 0 0] [ 1 1 1 1] [ 1 -1 1 -1] [ 2 0 2 0] [ 1 1 -1 -1] [ 2 2 0 0] [ 2 0 0 -2] [ 3 1 1 -1] [ 1 -1 -1 1] [ 2 0 0 2] [ 2 -2 0 0] [ 3 -1 1 1] [ 2 0 -2 0] [ 3 1 -1 1] [ 3 -1 -1 -1] [ 4 0 0 0] [0 0 0 0] [0 0 0 0] [0 1 0 1] [0 1 0 1] [0 0 1 1] [0 0 1 1] [0 1 1 0] [0 1 1 0] [0 1 1 0] [0 1 1 0] [0 0 1 1] [0 0 1 1] [0 1 0 1] [0 1 0 1] [0 0 0 0] [0 0 0 0] 0 0 1 1 2 2 3 3 3 3 2 2 1 1 0 0 0 s s 1 s 1 2 s s 2 1 s 1 s s 0 3-ary Dull tribes are gray or red:        0        1        2        3 Sharp tribes are white.

3-ary_Boolean_functions#Walsh spectrum, 4-ary_Boolean_functions#wec

patron

The patron of a truth table is the XOR of itself and its twin. It is a noble.    (3-ary images)

praetor

XOR of left and right half of the TT.    (3-ary images)

quaestor

XOR of left and reversed right half of the truth table (i.e. of the coordinates in the Hasse matrix)    (3-ary images)

principalities and dominions

	truth tables	Zhegalkin indices
principality
dominion

A principality is a set of n-ary truth tables whose (n+1)-ary noble equivalents form a faction.
Dominions are closely related to them. The reversed truth tables of the principalities are the Zhegalkin indices of the dominion.

The following table shows the six members of the red principality, which are also shown in the matrices on the right.
A representative of the 4-ary noble faction can be seen in the bottom left corner of this image.
(It is easily seen, that this tetrahedron can be permuted into six different positions.)

3-ary			4-ary noble
TT		Ж
0001 0000	8	136	0000 0001 0001 0000	2176
0000 0100	32	160	0000 0001 0000 0100	8320
0001 0100	40	40	0000 0000 0001 0100	10240
0000 0010	64	192	0000 0001 0000 0010	16512
0001 0010	72	72	0000 0000 0001 0010	18432
0000 0110	96	96	0000 0000 0000 0110	24576

An overview of all 11 3-ary principalities and dominions can be seen here.
Interesting subsets are those with entries on the diagonal and in the top row of the matrix of Zhegalkin indices.