Introduction to Elasticity/Disk with hole

From Wikiversity

Jump to: navigation, search

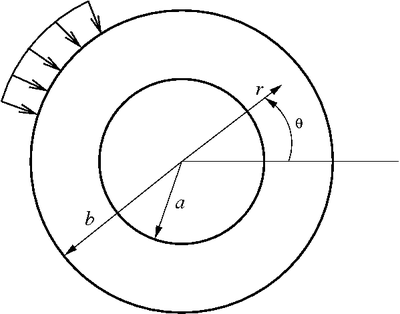
[edit] Disk with a central hole

An elastic disk with a central circular hole

Under general loading, for the stresses and displacements to be single-valued and continuous, they must be periodic in θ, e.g., σ11(r,θ) = σ11(r,θ + 2mπ).

An Airy stress function appropriate from this situation is

\text{(83)} \qquad \varphi = \sum^{\infty}_{n=0} f_n(r) \cos(n\theta) + \sum^{\infty}_{n=0} g_n(r) \sin(n\theta)

In the absence of body forces,

\text{(84)} \qquad \nabla^4{\varphi} = \nabla^2{(\nabla^2{\varphi})} = 0 ~;~~ \nabla^2{} = \left(\cfrac{\partial^2}{\partial r^2} + \cfrac{1}{r}\cfrac{\partial}{\partial r} + \cfrac{1}{r^2}\cfrac{\partial^2}{\partial \theta^2}\right)

Plug in \varphi.

\begin{align} \nabla^2{\varphi} = & \sum^{\infty}_{n=0} \left[ f^{''}_n(r) \cos(n\theta) + \cfrac{1}{r} f^{'}_n(r) \cos(n\theta) - \cfrac{n^2}{r^2} f_n(r) \cos(n\theta) \right] + \\ & \sum^{\infty}_{n=0} \left[ g^{''}_n(r) \sin(n\theta) + \cfrac{1}{r} g^{'}_n(r) \sin(n\theta) - \cfrac{n^2}{r^2} g_n(r) \sin(n\theta) \right] \qquad \text{(85)} \end{align}

or,

\text{(86)} \qquad \nabla^2{\varphi} = \sum^{\infty}_{n=0} F_n(r) \cos(n\theta) + \sum^{\infty}_{n=0} G_n(r) \sin(n\theta)

Therefore,

\begin{align} \nabla^4{\varphi} = & \sum^{\infty}_{n=0} \left[ F^{''}_n(r) \cos(n\theta) + \cfrac{1}{r} F^{'}_n(r) \cos(n\theta) - \cfrac{n^2}{r^2} F_n(r) \cos(n\theta) \right] + \\ & \sum^{\infty}_{n=0} \left[ G^{''}_n(r) \sin(n\theta) + \cfrac{1}{r} G^{'}_n(r) \sin(n\theta) - \cfrac{n^2}{r^2} G_n(r) \sin(n\theta) \right] \qquad \text{(87)} \end{align}

To satisfy the compatibility condition \nabla^4{\varphi} = 0, we need

\begin{align} \text{(88)} \qquad F^{''}_n(r) + \cfrac{1}{r} F^{'}_n(r) - \cfrac{n^2}{r^2} F_n(r) & = 0 \\ \text{(89)} \qquad G^{''}_n(r) + \cfrac{1}{r} G^{'}_n(r) - \cfrac{n^2}{r^2} G_n(r) & = 0 \end{align}

The general solution of these Euler-Cauchy type equations is

\begin{align} \text{(90)} \qquad F_n(r) & = A_1 r^n + B_1 r^{-n} \\ \text{(91)} \qquad G_n(r) & = C_1 r^n + D_1 r^{-n} \end{align}

We can use either to determine fn(r). Thus,

\text{(92)} \qquad f^{''}_n(r) + \cfrac{1}{r} f^{'}_n(r) - \cfrac{n^2}{r^2} f_n(r) = A_1 r^n + B_1 r^{-n}

or,

\text{(93)} \qquad r^2 f^{''}_n(r) + r f^{'}_n(r) - n^2 f_n(r) = A_1 r^{n+2} + B_1 r^{-n+2}

The homogeneous and particular solutions of this equation are

\begin{align} \text{(94)} \qquad f^h_n(r) & = A_2 r^n + B_2 r^{-n} \\ \text{(95)} \qquad f^p_n(r) & = A_1 r^{n+2} + B_1 r^{-n+2} \end{align}

Hence, the general solution is

\text{(96)} \qquad f_n(r) = A_1 r^{n+2} + B_1 r^{-n+2} + A_2 r^n + B_2 r^{-n}

This form is valid for n > 1. If n = 0,1, alternative forms are obtained. Thus,

\begin{align} \text{(97)} \qquad f_0(r) & = A_O r^2 + B_0 r^2 \ln r + C_0 + D_0 \ln r \\ \text{(98)} \qquad f_1(r) & = A_1 r^3 + B_1 r + C_1 r \ln r + D_1 r^{-1} \\ \text{(99)} \qquad f_n(r) & = A_n r^{n+2} + B_n r^n + C_n r^{-n+2} + D_n r^{-n} ~,~~n > 1 \end{align}

Terms in fn are chosen according to the specific problem of interest.

[edit] Traction BCs

at r = a
\text{(100)} \qquad \sigma_{rr} = T_1(\theta) ~,~~ \sigma_{r\theta} = T_2(\theta)
at r = b
\text{(101)} \qquad \sigma_{rr} = T_3(\theta) ~,~~ \sigma_{r\theta} = T_4(\theta)

Express Ti(θ) in Fourier series form.

\text{(102)} \qquad T_i(\theta) = \sum^{\infty}_{n=0} A_{ni}\cos(n\theta) + \sum^{\infty}_{n=0} B_{ni}\sin(n\theta) ~,~~i=1,2,3,4

Terms in Ti are chosen according to the specific problem of interest.

Retrieved from "http://en.wikiversity.org/wiki/Introduction_to_Elasticity/Disk_with_hole"