Fundamentals of probability and statistics

Why statistics are used

Statistics provide a way to describe the behavior of a person or thing or a collection of persons or things. For instance, sport statistics are used to describe the sports performance of players of the sport. Knowing that one baseball player is a .300 hitter while another player is batting .210 can help a baseball coach know which player needs additional help to improve their batting average.

Statistics provide a way for a person to make decisions when the person is uncertain about the things or quantities involved in a decision. For instance, statistics are used in the insurance industry to make decisions about the insurability of people or things as well as to determine the rate to charge for the insurance. Statistics are used in determining the length of product warranties and to track how good sports players are. The use of statistics are good for making decisions involving the stock market and which lottery tickets to buy.

History of Statistics

Statistics were, in a way, studied by the Ancient Greeks. However, statistics began in earnest during the 1600s.

History of Probability

If we consider that man has evolved through the ages, that is Stone Age, Bronze Age and Iron Age, then we could have a basis of discussion.

Probability is a way of expressing knowledge or belief that an event will occur or has occurred. Probability may actually have a history not defined. Looking at the definition of probability;the likely occurance of an event (define as you find appropriate), it seems to have existed before man walked the earth. The decisions that are made in today's life are all based on the facts of their being likely to occur. Similarly, decisions that were made in stone age, Bronze Age or Iron Age were also based on the facts of occurrence,and the likelihood of their success or failure. In the early ages, there were no generalised educated definitions for probability

This means that every decision, has an element of probability in it. This only implies that from the time man was in the primitive stage to start using tools, probability was playing a vital role. Because there were chances that the tools and methods that were going to be used, could or could not work. Just like dressing up does not necessarily guarantee warmth as a function of clothing, some people dress up for fashion's sake not for either covering up or warmth.

Animals also use probability for their survival. They go hunting expecting to catch prey, or find a meal for themselves. But, there is a possibility that they might or might not catch their prey_ Their success and failure is measured by their instincts to survive or fight of which they do not have a guarantee of success. Taking an example of lions, when they catch prey they have a high success rate that they will have it all; but a school of hyenas due to their large numbers (one hyena will fail) will always scare the lions off their meal.

Mordern day mathematicians, however, have studied many systems and have come up with the formulae that would help one make constructive decisions about certain occurrences. Take an example of lotto tickets, every set of six numbers drawn have a chance of one in more than 12 million chances to win the jackpot; the lotto gurus suggest that one who at least plays 72 sets will reduces the base the more sets played, the higher the chances of winning. The stock exchange decisions and Investment decision are made all basing on the fact that using certain modules there is a higher probability of their success.

For The educated and modern definition and history, please view:http://en.wikipedia.org/wiki/Probability_theory#History

From Ssemondo

Variables and Measurements

There are two basic concepts for a person studying statistics to know and understand: what is a variable and what is a measurement.

A variable represents something which can change. For instance, if we are wanting to determine the batting average of a baseball player, two variables would be (1) number of hits and (2) number of times at bat. To calculate the batting average for a baseball player you must observe the desired behavior, ability to hit the ball successfully, and take measurements of the behavior. In this case the ability to hit the ball is computed by taking measurements of two variables, the number of times the baseball player is batting and the number of times when the baseball player is able to hit the ball successfully.

Different players will have different measurements or counts for these two variables. Some players will hit more often than other players. Some players may miss games due to illness or injury so have fewer times at bat.

Other examples of variables are:

• number of meals served in a restaurant
• price of houses in a neighborhood
• miles driven per gallon of gas consumed
• number of students in a classroom
• type of pie served in a restaurant
• high and low temperature for the day

Notice that of this list of variable examples, the types of measurements are different. Some such as number of meals served in a restaurant are counts, the meals are counted. Some such as price of houses in a neighborhood are financial figures or amounts, the amount of money someone paid for a particular house. Some, such as type of pie served in a restaurant, are types meaning that they are not really numbers at all but are classifications of objects (apple pie, chocolate pie, banana cream pie).

There are four different kinds of measurements. Each of these different kinds have different uses in statistical procedures. Some types of statistical procedures are used only with certain kinds of measurements.

The four kinds of measurements [[[w:Level of measurement]]] are:

• Nominal measurement. The numbers are actually placeholders for names, can be replaced by names, and usually are. Nominal measurements can be compared to see if they are equal or unequal, the same or different. There is no other kind of comparison that can be made with nominal measurements. This type of measurement can be remembered as "nominal means named".
• Ordinal measurement. The numbers are like nominal measurements with another added feature, ordinal measurements have rank or order. Ordinal measurements can be compared to see if they are equal or unequal. They can also be compared to see if one is less than or greater than the other. However, two ordinal measurements can not be added to each other or subtracted from each other. Ordinal measurements do not have standard intervals. This type of measurement can be remembered as "ordinal means ordered nominal".
• Interval measurement. The numbers are like ordinal measurement with another added feature, interval measurements are separated by the same interval. This means that interval measurements are based on a standard scale making arithmetic such as addition and subtraction possible. Interval measurements can be compared to see if they are equal or unequal. They can also be compared to see if one is less than or greater than the other. In a comparison, not only can you say one is greater than the other but that you can say how many units greater. This type of measurement can be remembered as "interval means ordinals with intervals".
• Ratio measurement. The numbers are like interval measurements with another added feature, ratio measurements have ratios between the possible measurement values. This means that ratio measurements are based on a standard scale which has a fixed zero point in which the zero point means zero amount.

To better explain the differences, lets take a look at examples of each of these different levels of measurements. In some of these cases we will also convert one level of measurement to another to help you understand the differences between the levels of measurements.

Examples of nominal measurements are:

• type of pie served in a restaurant. The pies served in the restaurant have different names such as chocolate pie, banana cream pie, apple pie (remember nominal means named)
• religious preference of students in a class. Each student has a particular religious preference such as Catholic, Baptist, Muslim, Hindu (remember nominal means named)

Examples of ordinal measurements are:

• finish position in a horse race. Each horse finishes in a sequence, first place, second place, third place (remember ordinal means ordered nominal)
• taste comparison of drinks. Flavor of drinks are compared and ranked in order of preference, first choice, second choice, third choice (remember ordinal means ordered nominal)

Examples of Interval measurements are:

• temperature in degrees Celsius. Because the Celsius temperature scale has an arbitrary zero point, the freezing point of water, you can compare 5 degrees Celsius to 10 degrees Celsius to see which is greater.

Examples of ratio measurements are:

• gallons of water used in flushing toilets. The scale for gallons of water has a non-arbitrary and specific zero point.
• number of slices of pizza eaten. The scale for number of slices of pizza eaten has a non-arbitrary and specific zero point.

Central Tendency and Descriptive and Inferential Statistics

There are two basic kinds of statistics. The first kind is descriptive statistics which are used to describe a sample or a population from which the sample is drawn. The second kind is inferential statistics which are used to infer from a sample characteristics of the population from which the sample is drawn.

Central tendency is the tendency or direction of a sample or a population. The central tendency is usually expressed as the mean though there are other statistics used to express central tendency. For instance a student's Grade Point Average (GPA) is a measure of central tendency, in this case the tendency of the student's ability to be a good student.

Descriptive statistics are the basic computations which we all know and learn quite early. The descriptive statistics can be divided into two major types, descriptions of the central tendency and descriptions of how much the measurements vary, the variance. Descriptions of central tendency are the arithmetic mean, the mode, and the median. Descriptions of variance are the variance, the standard deviation, and the range.

dependent variables. Typically, the question one attempts to answer using statistics is that there is a relationship between two variables. To demonstrate that there is a relationship the experimenter must show that when one variable changes the second variable changes and that the amount of change is more than would be likely from mere chance alone.

There are two ways to figure the probability of an event. The first is to do a mathematical calculation to determine how often the event can happen. The second is to observe how often the event happens by counting the number of times the event could happen and also counting the number of times the event actually does happen.

The use of a mathematical calculation is when a person can say that the chance of the event rolling a one on a six sided die is one in six. The probability is figured by figuring the number of ways the event can happen and divide that number by the total number of possible outcomes. Another example is in a well shuffled deck of cards, what is the probability of the event of drawing a three. The answer is four in fifty two since there are four cards numbered three and there are a total of fifty two cards in a deck. The chance of the event of drawing a card in the suite of diamonds is thirteen in fifty two (there are thirteen cards of each of the four suites). The chance the event of drawing the three of diamonds is one in fifty two.

Sometimes, the size of the total event space, the number of different possible events, is not known. In that case, you will need to observe the event system and count the number of times the event actually happens versus the number of times it could happen but doesn't.

For instance, a warranty for a coffee maker is a probability statement. The manufacturer calculates that the probability the coffee maker will stop working before the warranty period ends is low. The way such a warranty is calculated involves testing the coffee maker to calculate how long the typical coffee maker continues to function. Then the manufacturer uses this calculation to specify a warranty period for the device. The actual calculation of the coffee maker's life span is made by testing coffee makers and the parts that make up a coffee maker and then using probability to calculate the warranty period.

Experiments, Outcomes and Events

The easiest way to think of probability is in terms of experiments and their potential outcomes. Many examples can be drawn from everyday experience: On the drive home from work, you can encounter a flat tire, or have an uneventful drive; the outcome of an election can include either a win by candidate A, B, or C, or a runoff.

Definition: The entire collection of possible outcomes from an experiment is termed the sample space, indicated as $\Omega$ (Omega)

The simplest (albeit uninteresting) example would be an experiment with only one possible outcome, say $A$. From elementary set theory, we can express the sample space as follows:

$\Omega =\{A\}$

A more interesting example is the result of rolling a six sided dice. The sample space for this experiment is:

$\Omega =\{1,2,3,4,5,6\}$

We may be interested in events in an experiment.

Definition: An event is some subset of outcomes from the sample space

In the dice example, events of interest might include
a) the outcome is an even number
b) the outcome is less than three

These events can be expressed in terms of the possible outcomes from the experiment:
a) : $\{2,4,6\}$
b) : $\{1,2\}$

We can borrow definitions from set theory to express events in terms of outcomes. Here is a refresher of some terminology, and some new terms that will be important later:
$\cup$ represents the Union of two events

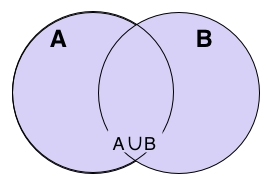
$\cap$ represents the Intersection of two events

$\{\cdots \}^{c}$ represents the complement of an event. For instance, "the outcome is an even number" is the complement of "the outcome is an odd number" in the dice example.
$A\backslash B$ represents difference, that is, $A$ but not $B$. For example, we may be interested in the event of drawing the queen of spades from a deck of cards. This can be expressed as the event of drawing a queen, but not drawing a queen of hearts, diamonds or clubs.
$\varnothing$ or $\{\}$ represent an impossible event
$\Omega$ represents a certain event
$A$ and $B$ are called disjoint events if $A\cap B=\varnothing$

Probability

Now that we know what events are, we should think a bit about a way to express the likelihood of an event occurring. The classical definition of probability comes from the following. If we can perform our experiment over and over in a way that is repeatable, we can count the number of times that the experiment gives rise to event $A$. We also keep track of the number of times that we perform the same experiment. If we repeat the experiment a large enough number of times, we can express the probability of event $A$ as follows:
$P(A)={\frac {N_{A}}{N}}$
where $N_{A}$ is the number of times event $A$ occurred, and $N$ is the number of times the experiment was repeated. Therefore, the equation can be read as "the probability of event $A$ equals the number of times event $A$ occurs divided by the number of times the experiment was repeated (or the number of times event $A$ could have occurred)." As $N$ approaches infinity, the fraction above approaches the true probability of the event $A$. The value of $P(A)$ is clearly between 0 and 1. If our event is the certain event $\Omega$, then for each time we perform the experiment, the event $\Omega$ is observed; $N_{\Omega }=N$ and $P(\Omega )=1$. If our event is the impossible event $\varnothing$, we know $N_{\varnothing }=0$ and $P(\varnothing )=0$.

If $A$ and $B$ are disjoint events, then whenever event $A$ is observed, then it is impossible for event $B$ to be observed simultaneously. For example, a number may either be odd or even, so the sets of odd and even numbers from 1 to 20 are disjoint events. Therefore, the number of times events $A$ union $B$ occurs are equal to the number of times event $A$ occurred plus the number of times $B$ occurs. This can be expressed as:
$N(A\cup B)=N(A)+N(B)$
Given our definition of probability, we can arrive at the following:
$P(A\cup B)=P(A)+P(B)$

At this point it's worth remembering that not all events are disjoint events. For events that are not disjoint, we end up with the following probability definition.
$P(A\cup B)=P(A)+P(B)-P(A\cap B)$
How can we see this from example? Well, let's consider drawing from a deck of cards. I'll define two events: "drawing a Queen", and "drawing a Spade". It is immediately clear that these are not disjoint events, because you can draw a queen that is also a spade. There are four queens in the deck, so if we perform the experiment of drawing a card, putting it back in the deck and shuffling (what statisticians refer to as sampling with replacement, we will end up with a probability of ${\frac {1}{13}}$ for a queen draw. By the same argument, we obtain a probability for drawing a spade as ${\frac {1}{4}}$. The expression $P(A\cup B)$ here can be translated as "the chance of drawing a queen or a spade". If we incorrectly assume that for this case $P(A\cup B)=P(A)+P(B)$, we can simply add our probabilities together for "the chance of drawing a queen or a spade" as ${\frac {1}{13}}+{\frac {1}{4}}$. If we were to gather some data experimentally, we would find that our results would differ from the prediction—the probability observed would be slightly less than ${\frac {1}{13}}+{\frac {1}{4}}$. Why? Because we're counting the queen of spades twice in our expression, once as a spade, and again as a queen. We need to count it only once, as it can only be drawn with probability of ${\frac {1}{52}}$. If we counted it twice with ${\frac {1}{13}}+{\frac {1}{4}}$, we will have to subtract it once: ${\frac {1}{13}}+{\frac {1}{4}}-{\frac {1}{52}}$. This reduces to ${\frac {4}{13}}$. Still confused?

Proof: If $A$ and $B$ are not disjoint, we have to avoid the double counting problem by exactly specifying their union.
$A\cup B=A\cup (B\backslash A)$ so
$P(A\cup B)=P(A\cup (B\backslash A))$
$A$ and $B\backslash A$ are disjoint sets. We can then use the definition of disjoint events from above to express our desired result:
$P(A\cup B)=P(A)+P(B\backslash A)$
We also know that
$P(B\backslash A)=P(B)-P(B\cap A)$
so
$P(A\cup B)=P(A)+P(B)-P(B\cap A)$
Whew! Our first proof. I hope that wasn't too dry.

Conditional Probability

• See also b:Probability/Conditional Probability

$P(even|prime)=1/3$
$P(prime|even)=1/2$

$P(even|prime)=1/4$
$P(prime|even)=1/5$

Many events are conditional on the occurrence of other events. Sometimes this coupling is weak. One event may become more or less probable depending on our knowledge that another event has occurred. For instance, the probability that your friends and relatives will call asking for money is likely to be higher if you win the lottery. In my case, I don't think this probability would change.

To obtain a formal definition of conditional probability, we begin with a working definition of probability: $P(A)={\frac {N_{A}}{N}}$ Consider an additional event $B$, and a situation where we are only interested in the probability of the occurrence of $A$ when $B$ occurs. A way at this probability is to perform a set of experiments (trials) and only record our results (that is: occurrence of $A$) when the event $B$ occurs. In other words
${\frac {N_{A\cap B}}{N_{B}}}$
We can divide through on top and bottom by $N$ the total number of trials to get $P(A\cap B)/P(B)$. We define this as 'conditional probability':
$P(A|B)={\frac {P(A\cap B)}{P(B)}}$
which when spoken, takes the sound "probability of $A$ given $B$."

Bayes' Law

An important theorem in statistics is Bayes' Law, which states that
$P(B|A)={\frac {P(A|B)P(B)}{P(A)}}$,
It is easy to prove. We start with identical expressions for $P(A\cap B)$.
We know that: $P(A\cap B)=P(B\cap A)$,
$P(A\cap B)={\frac {P(A|B)}{P(A)}}$, and
$P(B\cap A)={\frac {P(B|A)}{P(B)}}$.
Since $P(A\cap B)=P(B\cap A)$,
${\frac {P(A|B)}{P(A)}}={\frac {P(B|A)}{P(B)}}$.
A Simple rearrangement of above line gives us Bayes' Law.

Independence

Two events $A$ and $B$ are called independent if the occurrence of one has absolutely no effect on the probability of the occurrence of the other. Mathematically, this is expressed as:
$P(A\cap B)=P(A)P(B)$.

Random Variables

It's usually possible to represent the outcome of experiments in terms of integers or real numbers. For instance, in the case of conducting a poll, it becomes a little cumbersome to present the outcomes of each individual respondent. Let's say we poll ten people for their voting preferences (Republican - R, or Democrat - D) in two different electorial districts. Our results might look like this:
$\{RRRDRRDRRR\}$ and $\{DDDDDRDDDD\}$
But we're probably only interested in the overall breakdown in voting preference for each district. If we assign an integer value to each outcome, say 0 for Democrat and 1 for Republican, we can obtain a concise summary of voting preference by district simply by adding the results together.

Discrete and Continuous Random Variables

There are two important subclasses of random variables: discrete random variable (DRV) and continuous random variable (CRV). Discrete random variables take only countably many values. It means that we can list the set of all possible values that a discrete random variable can take, or in other words, the number of possible values in the set that the variable can take is finite. If the possible values that a DRV X can take are a0,a1,a2,...an, the probability that X takes each is p0=P(X=a0), p1=P(X=a1), p2=P(X=a2),...pn=P(X=an). All these probabilities are greater than or equal zero.

For continuous random variables, we cannot list all possible values that a continuous variable can take because the number of values it can take is extremely large. It means that there is no use to calculate the probability of each value separately because the probability that the variable takes a particular value is extremely small and can be considered zero P(X=x)=0).

Expected Value

Expected value is a generalization of the concept of "average" to included "weighted averages". It is often denoted as E(X), but the overline and bracket notation is also used.

Example: Consider the following calculation of the average value of X if X_i take on these three values {1, 3, 3, 5}. Using the overline to denote "average" (or "mean" or "expectation value"), we have:

$E(X)=\langle X\rangle ={\overline {X}}={\frac {\sum _{i=1}^{N}X_{i}}{N}}={\frac {1+3+3+5}{4}}$

We can also group these by the number of times each number appears, using $w_{i}$ to denote the "weight", or number of times each value of X_i is repeated.

${\overline {X}}={\frac {\sum _{i=1}^{N}w_{i}\cdot X_{i}}{N}}={\frac {1\cdot 1+2\cdot 3+1\cdot 5}{N}}={\frac {12}{4}}=3$

Factor the N inside the sum:

${\overline {X}}=\sum _{i=1}^{N}{\frac {w_{i}}{N}}\cdot X_{i}={\frac {1}{4}}\cdot 1+{\frac {2}{4}}\cdot 3+{\frac {1}{4}}\cdot 5$

Suppose you randomly selected one of the values in the set, {1, 3, 3, 5}. The probability of selecting a 3 is 50% because 2 out of four of the elements equal 3. Letting P denote probability, we have P(3) = 2/4 = 50%, and P(1) = P(5) = 1/4. Defining the probability,

${\overline {X}}=\sum _{i=1}^{N}P_{i}\cdot X_{i}$   where   $P_{i}={\frac {w_{i}}{N}}$

See also

• Topic:Statistics
• Introduction to research
• Statistical Economics
• Topic:Actuarial mathematics
• Introduction to Likelihood Theory
• Introduction to Classical Statistics
• Wikiversity:Statistics 202
• Introduction to probability and statistics
• Bayesian Statistics
• Statistics for Business Decisions

Offsite courses

With video lectures

1. Probability and Random Processes, Mrityunjoy Chakraborty, IIT Kharagpur, 2004.
2. Probability Primer, mathematicalmonk, YouTube
3. Probabilistic Systems Analysis and Applied Probability, John Tsitsiklis, Massachusetts Institute of Technology, Fall 2010

Without videos lectures

1. Fundamentals of Probability, David Gamarnik and John Tsitsiklis, Massachusetts Institute of Technology, Fall 2008.
2. Applied Probability and Stochastic Modeling, Edward Ionides, University of Michigan, Fall 2013
3. Probability and Statistics I , Motoya Machida, Tennessee Tech University, Fall 2010
4. Probability and Statistics II , Motoya Machida, Tennessee Tech University, Spring 2011
5. Probability and Random Processes, Tara Javidi, University of California, San Diego, 2012.
6. Introduction to Statistical Methods, Joseph C. Watkins, University of Arizona, Spring 2013
7. Probability Theory, Jenny Baglivo, Boston College, Fall 2013.
8. Mathematical Statistics, Jenny Baglivo, Boston College, Fall 2013.
9. Modern Statistics, Jenny Baglivo, Boston College, Spring 2014
10. Probability, Colin Rundel, Duke University, Spring 2012.
11. Applied Probability, Matthias Winkel, Oxford University, 2012.
12. Probability, Frank King, University of Cambridge, 2007–08.
13. Nonparametric Methods, Tom Fletcher, Utah University, Spring 2009.
14. Communication Theory, B. Srikrishna, IIT Madras, Jul-Nov 2007.

Formula sheets

1. Probability Formula Sheet by Colin Rundel
2. Theoretical Computer Science Cheat Sheet
3. Probabilistic Systems Analysis Cheat Sheet by Gowtham Kumar
4. Probability and Statistics Cookbook by Matthias Vallentin, 2012
5. Review of Measure Theory by Joel Feldman, 2008
6. A Probability Refresher by Vittorio Castelli.
7. Cheat Sheet for Probability Theory by Ingmar Land, 2005
8. Combinatorics Cheat Sheet by Lenny Pitt

Other resources

1. Probability and Statistics, Wolfram MathWorld
2. e-Statistics, Dept of Maths, Tennessee Tech University.
3. Online Statistics Education by Rice University (Lead Developer), University of Houston Clear Lake, and Tufts University
4. Category:Probability theory paradoxes, Wikipedia
5. Category:Probability Theory, ProofWiki.
6. Notes on Financial Engineering, K. Sigman, Columbia University.
7. Probability by Surprise by Susan Holmes
8. GameTheory.net
9. Java Applets provided by James W. Hardin
10. Java applets for power and sample size by Russ Lenth
11. Web Interface for Statistics Education at Claremont Graduate University