Binary Stars and Extrasolar Planets

This learning activity utilizes text, imagery, and applet-simulations to introduce the concepts associated with Binary Star systems and the search for Extrasolar Planets (exoplanets for short). This is a rapidly developing field within Astronomy due to new technology allowing scientists to either directly image or better infer the presence of exosolar planets via gravitational pull, detection of change in visual magnitude, and other methods.
The activity is separated into three parts to contour the experience into basic, advanced, and mathematical conceptual understanding. The basic level will introduce the general ideas of what is occurring. The advanced level will further the conceptual experience to fully understanding the concepts necessary to apply mathematical analysis upon either a binary star system or exoplanet. The mathematical analysis will introduce Astrophysics equations in order to give a taste of how scientists analyze the data they collect to aid in the discovery of exoplanets. Lastly, if you still seek more there is a way that you too can aid in the search for exoplanets without the need for a degree in the field or a large telescope!
When you have completed this activity you should be able to; by level: Basic: Know terminology and have background-level knowledge of binary systems and exoplanets. Advanced: Know and understand select techniques pertaining to binary systems and how they can be applied to the search for exoplanets. Mathematical: Be able to use data to get practical information about either binary stars or exoplanets.
Basic Concepts:
[edit | edit source]This section looks into the types of binary stars, the light curve, center of mass, and a simple applet to understand how changing mass and distance causes changes in the orbits of binaries.

Types of Binary Stars:
- Optical Double: This is actually better used to actually define what constitutes a binary star. This is not a binary star system and is actually just stars that appear close to each other based upon our vantage point and can be, often are, very far apart. Thus, the definition of a binary star requires that the stars are gravitationally bound like the Earth and the other planets in our Solar System are to the Sun.
- Visual Binary: This describes two gravitationally bound stars that are one of or a combination of the following: bright enough, far enough apart, and/or near enough to be seen separately by high-powered telescopes. Albireo, Mira, and Sirius are three examples of visual binaries and have images displaying both stars. Note that more stars can also be present, Polaris (the North Star) is actually a ternary system (three stars) with visual verification.
- Astrometric Binary: Only one star is visible through current telescopes, but the movement of the star from the gravitational pull of the other star indicates the presence of its unseen companion star. It is a system in which a visible star and a dimmer companion orbit a common centre of mass and detection of such binary by astrmetric means are called astrometric binary.
- Eclipsing Binary: Eclipsing binary stars means that the star system is oriented, from our vantage point, in such a way that one star passes in front of the other and then later passes behind the other. This is most notably recognized by a reduction in light due to the one passing in front of the other blocking some or all of the light from the one behind while when both remain visible they both show their entire light output. Algol, β Perseus, also known as the Demon star are the first eclipsing binary.
- Spectroscopic Binary: A spectrum of light at rest produces wavelengths that remain at the same wavelength under all stationary conditions. However, when moving towards or away from the observer this spectrum shifts. This method uses the spectra received from stars to note shifts in the position of the bands. We are then able to know when a star is moving away (shifts the spectrum towards the red end) or towards us (towards blue end). This is aptly termed red shift and blue shift.
All of the above, with the exception of an optical double, can also be applied for exoplanet discovery although the size, mass, and light emission for exoplanets make it considerably more difficult. Optical doubles are impossible for exoplanets since the overwhelming majority of their light is reflected from the star they orbit.
The Light Curve
[edit | edit source]
As shown, the light curve over the period (the length of the line) of orbit has two drops in luminosity. This would be the data generated by an eclipsing binary star system.
The first drop is far greater, indicating that it is the passing of the colder, less luminous star in front of the hotter one. This means that, for every unit area, it is in effect blocking more light. It does not matter which star, colder or hotter, is larger.
The second drop represents the hotter star passing in front of the cooler one. It is less because the light being blocked is that of the less luminous star which for every unit area sends less light towards the observer than the hot one.
The duration of the drops should be approximately the same (not perfectly reflected in this image) as the smaller star disappears at the same rate behind as it blocks the light in front. Also, the duration reflects the time spent behind or in front of the other star. The diagonal slopes in and out represent the partial concealment of the star being progressive depending on the duration it takes to fully block the other star.
Again, this can be applied to exoplanets, albeit far more difficult. Although the lack of light production by a planet assists by decreasing the luminosity to nearly nothing for the gap it makes, the gap of light it actually makes is so much smaller due to tiny radius relative to that of a star that it is nearly unnoticeable to even many modern telescopes.
Center of Mass
[edit | edit source]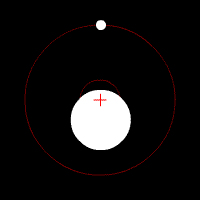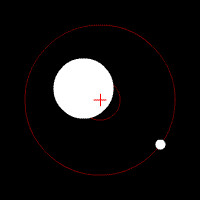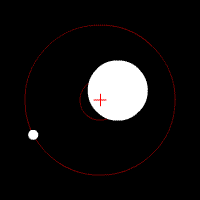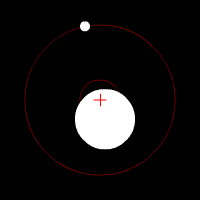
Center of mass is a point at which the combined mass of the two (or more) bodies involved in the rotation act as if they were concentrated at this single point. This point lies between the masses involved, and is closer to the larger masses then the smaller masses. If the system of rotating masses has a transverse velocity the motion can be represented by the motion of the center of mass with this same velocity. This can be related to the solar system in the sense that the Sun is (essentially, it too rotates some, in actuality, from the pull of the planets) the center of mass by which the planets orbit. However, when two bodies approach nearer masses this point is drawn out of being located within the heavier body and actually lies at a point in space directly between the two bodies. It remains equidistance from both stars (in the case of exactly equal mass) as the orbit in their elliptical orbits about it. The figure shows a center of mass located within the star, but note that they always remain on opposite sides of the center. More bodies makes the situation far more complex, but ultimately it is the same idea that at any given time the positional motion of all the bodies keeps the central rotation about the center of mass.
Application of Basic Ideas
[edit | edit source]We now turn to the Applet to gain an active appreciation for the above concepts. To keep things simple, the Applet for this section has limited options. Once you open it, you can see the white dot as the star (the Sun for most of the options) and the blue dot as the planet. The Applet also greatly exaggerates the movement about the center of mass to exemplify the effect of gravitational binding between the two objects making them both move. One must be aware of this as the 10 Jupiter setting demonstrates the movement of two near-equal mass bodies whilst in reality ten times the mass of Jupiter is still a very miniscule mass compared to the sun (a mere 0.95%) and would not send the Sun on a crash-course through the solar system as this Applet shows.
Now, let’s run some tests with the Applet[1] (Open in new window if it fails to run in a new tab) and see if you can answer the questions posed correctly.
- Run the simulation for a while with the standard set up of Sun/Jupiter. Then switch to the Sun/Earth. What do you notice about the center of mass? Set to Sun/Jupiter again and observe then switch to two Jupiters, then five Jupiters. What changes happen with each change in the mass ratio?
- Let us suppose this is a visual binary system and two stars orbiting instead of a star and a planet. What would we be able to determine about the masses based on watching the rotation? If one or the other was not visible, would we still know it was a binary system? What type of binary system would it be?
- Suppose we were looking at this as a spectroscopic binary. Would we be able to determine anything based on spectra obtained from repeatedly viewing this binary system?
- Let us suppose it’s an eclipsing binary. If our vantage point was from the bottom of the screen, at what position(s) in the orbit would we see a dip in light? What about if our vantage point was from the right?
Answers:
- The center of the mass is inside the Sun when it is using the Earth because the difference of mass is so great, but with Jupiter it was not (remember that in reality it is always within the Sun though, regardless of the planets’ alignment). As the mass ratio increases the simulation leaves the center of mass at the center of rotation and Jupiter remains at the same location, but the Sun moves further away from the center of mass to maintain the center of mass at a proper distance relative to the mass ratio.
- We would know that the one moving less is more massive. It would be a spectroscopic binary system because we would only see one star wobbling back and forth in space.
- No, we would not be able to determine anything because it has no motion towards or away from us and just maintains a flattened appearance. Note, however, that this situation of perfectly perpendicular is very unlikely in practicality and some shift would likely be able to be obtained if the motion was fast enough.
- At the bottom and the top when the two bodies are aligned from our vantage point. When we were observing from the right, it would be when the stars were on the right and left side of the orbit. Note that, matter where we placed the vantage point, there would always be two spots in which the light would be reduced and both would be when they came into alignment from our vantage point.
That concludes the basics of binary stars and exoplanets. We now move on to flesh out more advanced concepts, some of which were alluded to here.
Advanced Concepts
[edit | edit source]This section looks into the more advanced concepts of: Kepler’s Laws of Planetary Motion, Newton’s version of Kepler’s Third Law, Orientation to Earth, Doppler Shift, and Proportionality.
Kepler’s Laws of Planetary Motion
[edit | edit source]
Kepler’s Laws were created to explain the motion of the planets in the Solar System. They are based upon Tycho Brahe’s very accurate measuring of the heavens over many years. They center on the principle of rejecting the geocentric model in favor of the heliocentric model as was necessary to match the data without using epicycles to explain the motion.
They are as follows:
- "The orbit of every planet is an ellipse with the sun at a focus."
- "A line joining a planet and the sun sweeps out equal areas during equal intervals of time."
- "The square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit."
The first law works on the principle of center of mass. Kepler determined the orbits were elliptical based upon Tycho’s measurements not fitting the theory using perfect circles which is logical to abide by today when dealing with binaries and exoplanets.
The second law is also useful by relating the speed increase when the objects interacting approach each other and slow when departing. Velocity is a useful tool towards determining other information about binary stars and stars with exoplanets.
The third law was the first true astrophysical equation. Although it only applies to objects orbiting the Sun (or other approximately equal mass stars) in its current form it is still useful and becomes greatly more useful when later manipulated by Newton. Kepler’s third law has become hugely helpful in determining the masses present in binary stars or exoplanets as will be used in the mathematical concepts portion.
The third law in proportional form:
- P in Years
- a in AU
Newton’s Law of Gravitation Applied to Kepler’s Third Law
[edit | edit source]Newton’s Law of Gravitation dictates that all objects in the universe are gravitationally bound to each other. This is drawn into Kepler’s Laws by the planet exerting a force on the star as well as the star on the planet and also separated the masses so one can apply the property to any objects that are gravitationally bound in a meaningful way (not so distant that the pull has no impact).
Newton’s revised law:
- P in Seconds
- a in Meters
- G is the Gravitational Constant: 6.673x10-11
- M and m in kilograms
This law is commonly used to determine the total mass of visual binaries that then allows extrapolation to large amounts of other data.

Orientation to Earth
[edit | edit source]The orientation to Earth is often known as inclination. The vast majority of stars provide an orientation of their satellites that is not eclipsing over the center of the star or perfectly upon the celestial sphere. It is for this reason that when we often are only able to extrapolate a minimum mass when viewing a star’s wobble because we do not know the inclination and, thus, are only able to detect the portion pulling the star on the plane of celestial sphere.
Doppler Shift
[edit | edit source]
Doppler Shift is the basis for a Spectroscopic Binary system. It is found by either two separate shifts in spectra or a single shift generated by an unseen companion on the primary star. It is important because the shifts can be used to find the radial velocity of both stars or the visible one if only one spectrum is observed. The equation to determine radial velocity is:
c is the speed of light in a vacuum (3x108 m/s)
λ0 is the rest wavelength of the spectra
Δλ is the change from the rest wavelength to the measured wavelength
vr is the radial velocity in m/s
If the period is known this can be paired with it to determine the semi-major axis.
Proportionality
[edit | edit source]Since all motion involving two objects revolves around a give-and-take relationship there arises the intrinsic relationship between many physical aspects of the two and their behavior with respect to each other.
All of the following relations can be derived from Kepler’s Laws and Doppler Shift and associated mathematical principles.
Note: Units do not matter as they are ratios and the units cancel.
m is mass
r is the separation distance
a is the length of the semi-major axis
α is the angular separation
v is the velocity
vr is the radial velocity
Δλ is the change in wavelength due to Doppler Shift
Application of Advanced Ideas
[edit | edit source]This application section will use a more technical Applet[2] that allows for more intimate manipulation of the model to better experiment with some of the ideas in this section.
- Leaving the model on the default settings, study the layout with radial velocity, the visible light spectrum, the earth view, and the privileged view. Observe the radial velocity and spectrum. How do they behave? What does the negative velocity indicate? Let the left (red end) rest wavelength be 650 nm. Calculate the shift in wavelength when the red and blue paths cross and when red peaks in the positive.
- Experiment with the model. First, adjust the values so that the privileged view is the same as the earth view. What impact does this have on the Doppler Shift? Second, adjust it to attain an eclipsing system. Lastly, make the following changes: a = .8, e = .8, i = 30, w = -45. Note the radial velocity curve now. Explain this velocity curve and note the difficulty of being able to understand it if one of the curves did not exist.
- Change the three solar mass star to be .0009535, Jupiter’s mass in terms of solar mass. Note the Doppler Shift for the star now. Explain what two changes can be made to the variables (not changing mass) that would aid in discovering this planet. One will be reflected in the model while the other will not readily do so.
- Formulate a way to prove the concept of center of mass will lie equidistant from both bodies under ideal conditions and test it with the model.
- Using Jupiter’s mass of 1.8986x1027 kg, the Sun's mass of 1.9891x1030 kg and average distance between them of 7.786x1011 m determine the period of Jupiter in seconds. Verify this value by using the simplifed version (5.2 AU, ~πx107 s in a year).
Answers:
- When the velocity is going into the positive the spectrum is revealing a redshift (moving away) and when it is negative it is showing a blueshift (towards). The negative velocity reflects the movement of the star towards the observer; this is Astronomer's customary view of the motion. When the paths cross the change is zero because that is the point at which radial velocity from the observer's point of view is zero. When the red is peaking in the positive (about 27 km/s) the change in wavelength is calculated to be 0.0585 nm. Work shown below.
- Making the inclination 0 makes them match. This makes the Doppler Shift nothing because they are moving perfectly in the plane of the celestial sphere. Eclipsing is attained by making the inclination 90 degrees. The radial velocity curve gets rather difficult to read. It is important to note that the intersections are still zero so we can be certain of that. Further, the spikes in speed are when they are the closest as reflected in Kepler's Laws dictating equal area in equal time. With only one curve it's visibly quite difficult to infer the other and we are unable to be absolutely certain of values generated about such a binary star.
- One change would be to decrease a and thereby bring the period down to a mere 0.03 years which would make observing the star for a couple days reveal an entire period worth of data so that an observer could recognize the fast, but small, wobble of the star. The other change would be to turn the inclination to 90 degrees so that it would become eclipsing and a dip in light could be spotted from the planet transiting the star.
- Set both masses to be the same. They will then follow the exact same path around each other.
- Answer worked out below and yes they do match up fairly closely.
Doppler Shift worked out:
can be rewritten
which equals
and yields
nm.
Kepler's Third Law worked out:
can be rewritten
which equals
and yields
s2 → s
The simplified version:
which equals
and yields
yr2 → yr
which simplifies to
yrsyr-1 s.
This concludes the advanced concepts that can be associated with binary stars and exoplanets. To fully explore the nature of these entities continue onto the mathematical concepts that will utilize real stellar data to extrapolate more data about binary stars.
Mathematical Concepts:
[edit | edit source]To Be Added
Further Exploration
[edit | edit source]If you are interested in doing further exploration of exoplanets and helping the scientific community in the process you can go to visit Systemic[3]. The Systemic site has a console to download[4] which contains radial velocity data for stars which are suspect or known to be supporting exoplanets. You are able, with the console, to match a curve to the data by adding planets and controlling the planetary mass and distance until it is a good fit for the data accumulated so far. Upon registering, you are able to submit the curve where the system will compare it to other curves for the same data set generated by other members and, ultimately, as more data becomes available and submissions narrow down possible candidates to the stellar movement your curve fitting may contribute to the verification of the existence of one or more exoplanets orbiting a distant star. For further explanation of the software, check out their tutorials[5].

















