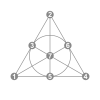
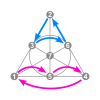
3-bit Walsh permutation/cycle shapes
 |
 |
|
2 2 (Europe) 2 4 (America) 3 3 (Asia) 7 (Africa) the four non-trivial cycle types | |
This table shows the 24 arrow patterns of the 168 3-bit Walsh permutations (as Fano plane collineations).
The typical shape of a collection is a hexagon, showing the two rotations and three reflections of some initial pattern.
The one pattern with rotational symmetry is shown as a pair. Patterns with mirror symmetry are shown as triangles.
Where the hexagon or triangle does not contain the inverse permutations, two nested polygons are shown.
These are the types of collections shown below:
- neutral permutation
- 1 pair (of rotations)
- 5 single triangles
- 1 double triangle
- 8 single hexagons
- 8 double hexagons
In the column graph, the shown permutations are highlighted in the respective component of the neighbor graph. All except 9 are in the cube-like clusters with 25 vertices. Apart from the center, there are four types of vertices, which are marked with suits.
Each permutation has a set of fixed points.
- The neutral permutation has only fixed points.
- 7-cycles have none.
- For cycle type 2+2 they form a line of the Fano plane.
- Cycle types 2+4 and 3+3 have single fixed points.
The points can be characterized by their binary weight, and the lines by the weights of their points. This property is in the column fixed.
| size | collection | graph | det | sum | cycles | fixed | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | + | 3 | ⊤ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
+ | 4 | 22 | 121 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
Rometranspose of Florence
|
+ | 5a | 22 | 121 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
Florencetranspose of Rome
|
+ | 5a | 22 | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
+ | 5b 6 |
24 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 |
|
+ | 3 | 33 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
New Yorktranspose of San Francisco
|
+ | 5a | 24 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
San Franciscotranspose of New York
|
+ | 5a | 24 | 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
+ | 4 | 7 | ⊥ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
Baghdadcompare Alexandria
inside: 5
|
+ | 5b 6 |
33 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
Alexandriacompare Baghdad
inside: b (5b)
|
+ | 5b 6 |
7 | ⊥ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
± | 7 | 7 | ⊥ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 * 2 |
|
± | 7 | 24 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
− | 3 | 22 | 132 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
Berlintranspose of Hamburg
|
− | 5a | 22 | 222 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 |
|
Hamburgtranspose of Berlin
|
− | 5a | 22 | 132 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
Beijingtranspose of Shanghai
|
− | 5a | 33 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
Shanghaitranspose of Beijing
|
− | 5a | 33 | 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
− | 4 | 33 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
Torontotranspose of Montreal
|
− | 4 | 24 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 |
|
Montrealtranspose of Toronto
|
− | 4 | 24 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
Delhitranspose of Mumbai
inside: 5
|
− | 5b 6 |
33 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
Mumbaitranspose of Delhi
inside: 5
|
− | 5b 6 |
33 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 * 2 |
|
− | 5b 6 |
7 | ⊥ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||