Selected topics in finite mathematics/Sets, logic, and arguments

[Give a very very brief overview of sets, logic, and arguments?]

Objectives[edit | edit source]

The objective is to understand the notion of sets and elements, as well as to understand how sets can be related to each other and to objects.

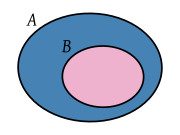
Details[edit | edit source]

Sets are any collection of things, like pens, pictures, schools, birds, shoes and much more. The objects within a set are called elements or members. A pen, for example, can belong to a set of writing utensils, but can also be a set itself as it is composed of parts. Sets are typically represented by circles and their element(s) by "X" in the form of a Venn Diagram, which uses overlapping circles to show similar and dissimilar characteristics.

Any sentence or claim that must either be true or false is a proposition or a statement, and can be represented by a Venn Diagram.

Logic is a type of reasoning and judgement that is used to solve problems.

[Describe something about logic?]

[Describe something about arguments?]

An argument made is only valid if the premises or assumptions that are used in the argument are feasible. If the assumptions are, it leads to a conclusion and is considered valid. The assumption that lead to a conclusion can be valid regardless of whether it is true or false. However, if the assumptions are found to be truthful and accurate the argument can be described as valid AND sound, thus producing a truthful conclusion.

[Describe something about validity?]

One way to use sets and logic to analyze if arguments are valid is to represent the argument with a Venn diagram.

[Describe how to use sets and logic to analyze the validity of an argument?]

Examples[edit | edit source]

Figure E1
Figure E2
Figure E3
Figure E4

Examples of sets and objects:

All cars = set
Bob's car = object
Trucks made by Ford = set
Alice = object
Yorkshire Terriers= set
New York City = Depends

This example would depend on what scenario New York City would be used in.

New York City could be a set if the statement about it was referring to the residents within the city.
New York City could be an object if the statement about it was referring to the other cities in the United States.

Examples of statements:

Bob is a person.
Alice is a car.
All universities are places of learning.
Some mustangs are cars.
2+2=4
2+2=5

If A is in B, B is in C, then A is in C

All students who are sick don't go to class, Alice is sick, therefore she must be a student

[Give an example of a sound argument?]

[Clean up the existing examples?]

Nonexamples[edit | edit source]

Examples of something that is not a set: a) A pen = this would be an object and not a set b) One shoe c) One balloon

Example of something that is not a statement: a) Do you like chicken? b) He drives 60 miles a week.

[Give an example of something that is not an argument?]

An example of an argument that is not a valid argument is: "All politicians are married, and John Smith is married. Therefore John Smith is a politician." This argument is not valid because John could still be married and not be a politician.

[Give an example of something that is not a sound argument?]

FAQ[edit | edit source]

[Ask a question?]

[Answer a question?]

Homework[edit | edit source]

[Make up a problem?]

Determine whether The university student body is best represented as a set, or an object.
Determine whether President Obama is best represented as a set, or an object.
Determine whether Squirrels is best represented as a set, or an object.

For each of the following statements, draw a Venn Diagram to represent it. Use common sense to determine if it is true or false, if possible.

All Americans are Human