Function (mathematics)
| Subject classification: this is a mathematics resource. |
| Type classification: this is a lesson resource. |
One of the most neglected topics in high school is the study of functions. In this lesson there are three rather lengthy chapters directly related to functions and several others that are indirectly related. There are two reasons for this: functions are important, and most calculus courses assume you know this topic almost perfectly, an unrealistic assumption. So let's get started at the beginning.
Introduction[edit | edit source]
We will start with an excruciatingly theoretical and general definition of a function in mathematics, and then look at the topic in a more down-to-Earth way.
Function: Given a set D. To each element in D, we assign one and only one element.
Example 1
The table below represents a function. 1 maps to a, 2 maps to 3, 3 maps to 3, and 4 maps to "pig". Each element in D is assigned one and only one element.
- "pig"
The set D is called the domain. There is a second set that arises, called the range. Notice that the domain and the range can contain the same thing (the number 3) or vastly different things (3 and "pig"). The domain and range are arbitrary mathematical sets. In this example, the domain is the set of integers 1 to 4, and the range might be the union of the set of integers, the set of letters, and the set of farm animals.
The rule (the arrows in the table above) is called the map or mapping. 1 is mapped into a; 2 is mapped into 3; 3 is mapped into 3; and 4 is mapped into "pig".
The true theoretical definition of a function is: A function is a domain, a range, and set of ordered pairs such that
- The first item in each pair is an element of the domain.
- The second item is an element of the range.
- No two pairs have the same first element. This property is sometimes expressed by saying that a function must be single valued.
- Every element in the domain appears as the first item of one (and only one) of the pairs.
In this example, the set of ordered pairs would be
A few things to note:
- It is perfectly legitimate for an element of the range to appear as the second item in more than one pair. That is, multiple domain elements can map to the same range element.
- Not every element of the range needs to appear as the second item in some pair. That is, there can be elements of the range that nothing maps to. In this example, no number maps to "cow", even though the range includes all farm animals. The subset of the range that consists only of those elements that do get mapped to is called the image. We will say more about that later.[1]
Example 2
This does not represent a function, since 1 would map to both a and d. It is not single-valued.
Function's Notation[edit | edit source]
The first depicts a function as sort of a "machine" that receives inputs and emits outputs. This is sometimes useful when dealing with composition of functions, as discussed below. The second depicts a function in terms of arrows going from points in the domain to points in the range. The diagram shows just 3 points in some very abstract representations of the domain and range.
If the function defined earlier is denoted f, we say: f(1) = a (read "f of 1 equals a"); f(2) = 3; f(3) = 3; and f(4) = "pig".
Mathematical notation
Where
- - Function of variable x
- - Function's variable
- - Function's value
Function Definition by a Rule[edit | edit source]
The definition of functions in terms of sets of ordered pairs is suitable only for abstract discussions of set theory. In practice, functions are usually defined by giving a rule, and having the domain and range be numbers. For example, here is a definition of a function whose domain and range are the real numbers:
If x is 2 then
Functions as Graphs[edit | edit source]
A way of visualizing functions that is extremely useful in practical situations, is as a graph. It only works for functions from real numbers to real numbers, but that is an extremely common case. The x-axis of the graph shows the domain, and the y-axis shows the range. A line of the required shape shows the function values (that is, y-values) for any given x-value.
The diagram below shows this (simultaneously) for two well-known trigonometric functions. The sine function is shown in red, and the cosine function in blue. Horizontal and vertical divisions are each 0.5.
Looking at the graph of a function makes it very easy to see a number of interesting characteristics, such as continuity. One can also estimate the derivative. For example, the graph on the right makes it quite plausible (and it is in fact true) that the derivative of the sine is the cosine, and the derivative of the cosine is the negative of the sine.
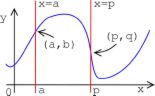
Inspection of a graph can also make it clear when a purported function does not satisfy the requirement of single-valuedness. A vertical line should cut the graph in only one place. The graph labeled "No" clearly doesn't satisfy that. One can see that it attempts to have f(p) = q and f(p) = r, which is not allowed.
Example 3
Let . The possible values of form the domain.
Let us assume that there are only three possible values of , that is, .
Then, the function converts these three values of into three different values of which form the set . The set is called the range of the function.
In this example, the three values that form the set are found to be
Therefore the range is . If we were to draw the points on a graph, we would have to graph (1,12), (-3,4) and (10,147).
NOTE
Instead of graphing points (x,y), we are graphing points (x,f(x)). For our purposes, the notation is different, but the meanings are the same.
Example 4
Let g(x) = x²-5x-9. D = {4,0,-3,,x+h}. Find the elements in the range.
This is a pretty crazy example, but there are reasons to do it.
g(4) = (4)²-5(4)-9 = -13
g(-3) = (-3)²-5(-3)-9 = 15
g(0) = 0²-5(0)-9 = -9
g() = ()²--9 = --9
g(x+h) = (x+h)²-5(x+h)-9 = x² + 2xh +h²-5x-5h-9 Wherever there is an x,
you replace it by x + h!
The range is {-13,-9,15, --9,x² +2xh +h²- 5x -5x -9}.
Example 5
If , find :
- (Add the fractions. Two tricks: a/b-c/d=(ad-bc)/bd;(e/f)/h=e/fh.)
- (Multiply out the top; never multiply out the bottom.)
- (Cancel the h's.)
This kind of problem occurs in almost every precalc book. What you should ask is why the heck it is here. I will tell you. This is very close to the topic you deal with in calculus. Here is a preview.
We have learned that the slope of a straight line is always the same. However, if we draw any curve and draw all its tangent lines, the slope changes. We would like to study this and algebraize it.
Given the point . A little bit away from P is point Q. Its x value is x + h, where x + h is an x value a little bit away from x. If the first coordinate is x + h, the second coordinate is f(x + h). Draw PQ, PR (horizontal line), and QR (vertical line). On any horizontal line all y values are the same. P and R have the same y values. Q and R have the same x values.
Since Q and R have the same x values, the length of QR, which is the change in y or Δy, is . Since P and R have the same y values, the length of PR, which is the change in x or Δx, is .
The slope of the secant line l2 joining the points P and Q is
which is why we study this expression. But here's the conclusion. If we let h go to 0, graphically it means the point [x+h,f(x+h)] gets closer and closer to [x,f(x)]. If we do this process to the left of P as well as here to the right of P, and if they both approach the line l_1, then what we have calculated is the slope of the tangent line l1 at the point [x,f(x)]!!!!! You have taken your first step into calculus!!!!!
1-1 function. 1-1 is a property we need occasionally.
DEFINITION
If f(a) = f(b), then a = b.
Examples 6 and 7
f(x) = 2x is 1-1, but g(x) = x² is not 1-1.
If f(a) = f(b), then 2a = 2b and a = b.
If g(a) = g(b), then a² = b². But a could equal b or -b; therefore, not 1-1.
One-to-One, Onto, One-to-One Correspondence, and Inverse Function[edit | edit source]
If every point in the range of a function is actually mapped to (that is, the range is the same as the image), the function is said to be onto. A fancy term for this is that the function is surjective or is a surjection.
If no two points in the domain map to the same value, the function is said to be one-to-one. A fancy term for this is that the function is injective or is an injection.
If a function is both one-to-one and onto, it is said to be a one-to-one correspondence. A fancy term for this is that the function is bijective or is a bijection.
When a function is a one-to-one correspondence, something interesting happens. Refer back to the four fundamental principles given earlier. The third principle is that no two pairs have the same first element. But if the function is one-to-one, no two pairs have the same second element either. The fourth principle is that every element in the domain appears as the first item of one of the pairs. But if the function is onto, every element of the range appears as the second item of one of the pairs. This means that, if the function is both one-to-one and onto, we can swap the domain and range, and swap the first and second items of each pair, and still get a function. That function is the inverse of the original function. A bijection is invertible. The inverse of the function f is written f -1. We have
- f ( f -1 ( x ) ) = x for all x
- f -1 ( f ( y ) ) = y for all y
Image and Inverse Image[edit | edit source]
It is sometimes useful to speak of all of the function values for an entire set of points in the domain. Normally, when we say y=f(x), we mean that x is a specific element of the domain (for example, a specific number), and y is the single element that x maps to.

But sometimes we want to write something like Y=f(X), where X is a whole set. In this case, Y is the whole set of function values for all elements of X.
Y=f(X) is called the image of X. It is illustrated in the diagram to the right. The horizontal black line along the bottom edge depicts an open interval that we wish to find the image of. The vertical black line along the right edge depicts the image. The part of the function graph forming the image is shown in blue; the rest of the graph is in red. The grey lines are visual guides.

Also, X is called the inverse image of Y, denoted X=f -1(Y). That is, f -1(Y) is the set of points that map into Y.
This is illustrated in the diagram to the right. The vertical black line along the right edge depicts an open interval that we wish to find the inverse image of. The horizontal black lines along the bottom edge depict the two open intervals comprising the inverse image. The part of the function graph forming the inverse image is shown in blue; the rest of the graph is in red. The grey lines are visual guides.
References[edit | edit source]
- ↑ Some authors use the term "range" to refer only to those items that are actually mapped to, rather than those items that could potentially be mapped to. That is, they us the terms "range" and "image" interchangeably. It's not important in practice. The "image" is the set that is important, and its meaning is unambiguous. It is the set of just those elements that are actually mapped to.




























![{\displaystyle [x,f(x)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12a8462eec12737a5e8148e8a8616c84a34aa123)













