Primary mathematics/Powers, roots, and exponents
Exponents[edit | edit source]
Exponents, or powers, are a way of indicating that a quantity is to be multiplied by itself some number of times. In the the expression 25, 2 is called the base and 5 is called the exponent, or power. 25 is shorthand for "multiply five twos together": 25 = 2×2×2×2×2 = 32. Notice that the exponent tells us how many bases to multiply, not how many multiplications to perform. (In fact, the number of multiplications is one less than the number of bases.) 25 is read "two raised to the fifth power" or simply "two to the fifth."
In general,
where there are n x's to be multiplied.
It is better to say that exponent is 1 multiplied by x n times, . This is permissible because factor 1 is multiplicative identity, adding it does not change the product yet enables the empty one, .
The definition of exponent corresponds to equivalent definition of multiplication: n is nothing more than x added to 0 n times,
You can even convert one to another, using #Properties of Exponents,
Squaring numbers[edit | edit source]
A convenient way to say that a number is to be multiplied by itself (for example 5×5) is to say that the number is squared. To help visualize this, picture a square which is 5 units long and 5 units wide. This square will then have an area of 52 or 25 square units. 52 can be read "five raised to the second" but is most commonly read "five squared."
Area of five rows by five columns = 5 × 5 = 52 = 25.
Table of perfect squares[edit | edit source]
You may want to memorize some perfect square numbers:
| Square | Result |
| 02 | 0 |
| 12 | 1 |
| 22 | 4 |
| 32 | 9 |
| 42 | 16 |
| 52 | 25 |
| 62 | 36 |
| 72 | 49 |
| 82 | 64 |
| 92 | 81 |
| 102 | 100 |
| 112 | 121 |
| 122 | 144 |
| 132 | 169 |
| 142 | 196 |
| 152 | 225 |
| 162 | 256 |
| 172 | 289 |
| 182 | 324 |
| 192 | 361 |
| 202 | 400 |
Cubing numbers[edit | edit source]
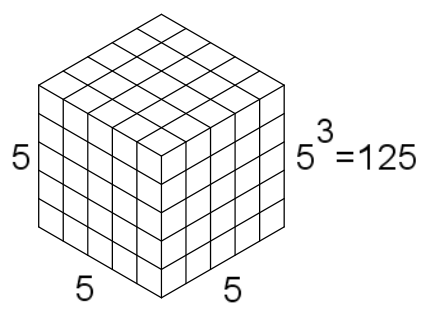
Similarly, a convenient way to say that a number is to be multiplied by itself and then itself again (for example 5×5×5) is to say that the number is cubed. To help visualize this, picture a cube which is 5 units long, 5 units wide, and 5 units high. This cube will then have a volume of 53 or 125 cubic units. 53 can be read "five to the third power" but is commonly read "five cubed."
Volume of a cube with height, width, and length of five = 5 × 5 × 5 = 53 = 125.
Table of perfect cube numbers[edit | edit source]
You may want to memorize some perfect cube numbers:
| Cube | Result |
| 03 | 0 |
| 13 | 1 |
| 23 | 8 |
| 33 | 27 |
| 43 | 64 |
| 53 | 125 |
| 63 | 216 |
| 73 | 343 |
| 83 | 512 |
| 93 | 729 |
| 103 | 1000 |
Higher powers[edit | edit source]
Numbers higher than three may also be used as exponents, although there is no common term for numbers raised to a fourth power or higher. For example, 54 = 5×5×5×5 = 625.
Table of higher powers[edit | edit source]
| xn | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | n |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 2n | |
| 3 | 1 | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | ||||||
| 4 | 1 | 4 | 16 | 64 | 256 | 1024 | 4096 | ||||||||
| 5 | 1 | 5 | 25 | 125 | 625 | 3125 | |||||||||
| 6 | 1 | 6 | 36 | 216 | 1296 | 7776 | |||||||||
| 7 | 1 | 7 | 49 | 343 | 2401 | ||||||||||
| 8 | 1 | 8 | 64 | 512 | 4096 | ||||||||||
| 9 | 1 | 9 | 81 | 729 | 6561 | ||||||||||
| 10 | 1 | 10 | 100 | 1000 | 10000 | ||||||||||
| 11 | 1 | 11 | 121 | 1331 | |||||||||||
| 12 | 1 | 12 | 144 | 1728 | |||||||||||
| 13 | 1 | 13 | 169 | 2197 | |||||||||||
| 14 | 1 | 14 | 196 | 2744 | |||||||||||
| 15 | 1 | 15 | 225 | 3375 | |||||||||||
| 16 | 1 | 16 | 256 | 4096 | |||||||||||
| ... | |||||||||||||||
| x | 1 | x | x2 | x3 |
Note: 00 is undefined.
Properties of Exponents[edit | edit source]
There are several properties of exponents which are frequently used to manipulate and simplify algebraic and arithmetic expressions.
It follows immediately that
-
()
-
()
and
-
()
These can be extended to multiple factors
Alternatively, we can use first property to obtain
-
()
and use others to write down
-
()
Bases and exponents of one and zero[edit | edit source]
Any number raised to an exponent of one equals itself. So, for example, 51 = 5.
Any non-zero number raised to an exponent of zero equals one. So, for example, 50 = 1.
Zero raised to any positive exponent is still zero. So, for example, 05 = 0.
One raised to any exponent is still one. So, for example, 15 = 1.
Zero raised to an exponent of zero is not defined.
Fractional powers[edit | edit source]
A base may also be raised to a fractional, or decimal power. This will be covered later in the lesson.
Roots[edit | edit source]
Roots are the inverse operation of powers (i.e. and from the properties of exponents we have ):
Square root[edit | edit source]
The inverse operation of squaring a number is taking the square root of that number. So, for example, the square root of 25 is the number which must be multiplied by itself to equal 25. In this case, the answer is 5. There are two types of notation used here:
Note, however, that most square roots don't yield integers, and many don't even produce rational numbers.
Manually finding a square root[edit | edit source]
One method for manually taking square roots is to repeatedly do long division. Let's take the square root of 10 in this example. We would start by estimating the answer. Since 32 = 9 and 42 = 16, we know the answer lies between 3 and 4. Furthermore, since 10 is only one away from 9, but is 6 away from 16, we could estimate that the answer is one-seventh of the way between 3 and 4. This won't give an exact answer, and a seventh is ugly to work with, so let's use a fifth, instead. This gives us 3 1/5 or 3.2 as a starting estimate.
Now do long division to divide 10 by 3.2. We get 3.125. The average of 3.2 and 3.125 is (3.2 + 3.125)/2 = 6.325/2 = 3.1625, so that will be our next estimate.
Now do long division to divide 10 by 3.1625. We get 3.162055... (we didn't really need to go more than one digit beyond the number of decimal places we started with). The average of 3.1625 and 3.1621 is 3.1623, so that will be our next estimate.
Now do long division to divide 10 by 3.1623. We get 3.162255...
So, this method can be repeated to get the desired level of accuracy. The actual square root of 10 is 3.16227766...
Note that calculators or computers are used for most square root calculations, but knowing how to manually calculate a square root can be quite useful when no calculator is available.
If you would like to try this method yourself, try finding the square root of 7.
Cube root[edit | edit source]
The inverse operation of cubing a number is taking the cube root of that number. So, for example, the cube root of 125 is the number which must be multiplied by itself and then multiplied by itself again to equal 125. In this case, the answer is 5. There are two types of notation used here:
Note, however, that most cube roots don't yield integers, and many don't even produce rational numbers.
Higher roots[edit | edit source]
Numbers higher than three may also be used as roots, although there is no common term for fourth roots or higher. For example:
Note, however, that most higher roots don't yield integers, and many don't even produce rational numbers.
Combining powers and roots[edit | edit source]
The unit fraction notation used for roots previously may have given you the idea that roots are really the same as powers, only with a unit fraction (one over some number) instead of an integer as the exponent. Thus, the fractional notation is actually preferred in higher mathematics, although the root symbol is still used occasionally, especially for square roots.
Fractions as exponents[edit | edit source]
Other (non-unit) fractions may also be used as exponents. In this case, the base number may be raised to the power of the numerator (top number in the fraction) then the denominator (bottom number) may be used to take the root. For example:
Alternatively, you can take the root first and then apply the power:
Decimal exponents[edit | edit source]
Any fractional exponent can also be expressed as a decimal exponent. For example, a square root may also be written as:
Also, decimals which can't be expressed as a fraction (irrational numbers) may be used as exponents:
Such problems aren't easy to solve by hand using basic math skills, but the answer can be estimated manually. In this case, since 3.1415926 is between 3 and 4 (and considerable closer to 3), we know that the answer will be between 5^3 (or 125) and 5^4 (or 625), and considerable closer to 125.
Negative exponents[edit | edit source]
A negative exponent simply means you take the reciprocal (one over the number) of the base first, then apply the exponent:
Alternatively, you can first apply the exponent (ignoring the sign), then take the reciprocal:
Fractions as bases[edit | edit source]
When a fraction is raised to an exponent, both the numerator and denominator are raised to that exponent:
Fractions may also be used for both the base and exponent:
In addition, negative fractional exponents may be used, taking the reciprocal of the base, as always, to find the solution.
Negative bases[edit | edit source]
Negative bases can be handled normally for integer powers:
Note that negative bases raised to even powers produce positive results, while negative bases raised to odd powers produce negative results.
Be careful with negative signs. Since -5 = -1×5, there is a difference between and . The former means the negative of 5 times 5, whereas the latter
means -5 squared. In other words,
but
Roots and fractional/decimal powers are a bit trickier. Odd roots work out fine:
Even roots, however, have no real solution:
Note that there is no real number, when multiplied by itself, which will produce -25, because 5×5 = 25 and -5×-5 = 25. There is actually a solution, called an imaginary number, but that won't be discussed until later lessons.
Principal root[edit | edit source]
Note that, since both 5×5 = 25 and -5×-5 = 25, when we are asked to take the square root of 25 there are, in fact, two valid answers, 5 and -5. Actually, any even root of a positive number will have two solutions, one positive and one negative. This may seem unusual, but, in higher mathematics, problems often have multiple solutions.
However, for many problems, only the positive value seems to physically work. For example, if we are asked to figure the length of the sides of a square yard which has an area of 25 square units, only 5 units on a side works. If we said "each side can also have a length of -5 units", that doesn't make any sense. For this reason, the positive solution is called the principal root, and, depending on the question, may be the only desired answer. In cases where either answer is valid, it is sometimes written as ±5 (read as "plus or minus five").












![{\displaystyle {\sqrt[{n}]{x^{n}}}=x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c2edf48b0011519cbf8743ba8b2c6b7db8c2cf7)
![{\displaystyle {\sqrt[{n}]{x}}=x^{1/n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bc8259648708fec070cf7e9572f399b4d8f6b9f)

![{\displaystyle {\sqrt[{3}]{125}}=125^{1/3}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2aa3f26e00133a4826fec2ebc32cb9d8d7c6532e)
![{\displaystyle {\sqrt[{4}]{625}}=625^{1/4}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f879adde6df2ab4e2fea9c469131e3c8fbeb4e4)
![{\displaystyle 8^{2/3}={\sqrt[{3}]{8^{2}}}={\sqrt[{3}]{64}}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11c211fd0f405449abdb26e4ca2812fbcb46dba1)
![{\displaystyle 8^{2/3}=({\sqrt[{3}]{8}})^{2}=2^{2}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7cd2c46220b46832c08f1646348ac3f1600a78d2)
















