Materials Science and Engineering/Doctoral review questions/Daily Discussion Topics/01082008

Omnidirectional Waveguide

Dielectric Mirror

A dielectric mirror is a type of a mirror composed of multiple thin layers of dielectric material, typically deposited on a substrate of glass or some other optical material. By careful choice of the type and thickness of the dielectric layers, one can design an optical coating with specified reflectivity at different wavelengths of light. Dielectric mirrors are also used to produce ultra-high reflectivity mirrors: values of 99.999% or better over a narrow range of wavelengths can be produced using special techniques. Alternatively, they can be made to reflect a broad spectrum of light, e.g. the entire visible range or the spectrum of the Ti-sapphire laser. Mirrors of this type are very common in optics experiments, due to improved techniques that allow inexpensive manufacture of high-quality mirrors. Examples of their applications include laser cavity end mirrors, hot and cold mirrors, thin-film beamsplitters, and the coatings on modern mirrorshades.

Dielectric mirrors function based on the interference of light reflected from the different layers of dielectric stack. This is the same principle used in multi-layer anti-reflection coatings, which are dielectric stacks which have been designed to minimize rather than maximize reflectivity. Simple dielectric mirrors function like one-dimensional photonic crystals, while others have a more complicated structure generally produced by numerical optimization. In the latter case, the phase dispersion of the reflected light can also be controlled.

The manufacturing techniques for dielectric mirrors are based on thin-film deposition methods. Common techniques are physical vapor deposition (which includes evaporative deposition and ion beam assisted deposition), chemical vapor deposition, ion beam deposition, molecular beam epitaxy, and sputter deposition. Common materials are magnesium fluoride, silicon dioxide, tantalum pentoxide, zinc sulfide (n=2.32), and titanium dioxide (n=2.4).

Perfect Mirror

A perfect mirror is a theoretical mirror that reflects light (and electromagnetic radiation in general) perfectly, and doesn't transmit or absorb it.

Domestic mirrors are not perfect mirrors as they absorb a significant portion of the light which falls on them.

Dielectric mirrors are glass or other substrates on which one or more layers of dielectric material are deposited, to form an optical coating. A very complex dielectric mirror can reflect up to 99.999% of the light incident upon it, for a narrow range of wavelengths and angles. A simpler mirror may reflect 99.9% of the light, but may cover a broader range of wavelengths.

Almost any dielectric material can act as a perfect mirror through total internal reflection. This effect only occurs at shallow angles, however, and only for light inside the material. The effect happens when light tries[say what?] to go from a medium with a higher index of refraction to one with a lower value (like air).

A new type of "perfect mirror", developed in 1998 by researchers at MIT, is a hybrid made of thin films of metals and dielectrics. These unusual mirrors are very efficient reflectors over a broad range of angles and wavelengths, and are insensitive to polarization.

Comments during Discussion

An infinite number of layers is a requisite of 100% reflectivity
The reflectivity is wavelength dependent
- The range of wavelengths highly reflected is about 100 nm
- Harmonics of frequencies are reflected
- Tune the wavelength that can transmit light
Use a large core to transmit a large amount of light
Materials are lossy
- Scattering between layers results in losses
- Attenuation: dB/km
Application: surgery
- Wavelength used: $10.6\mu m$ $10.6\mu m$
  - Low penetration depth
  - Local heating
Fibers incorporate multiple materials
- Materials chosen to add functionality
The structure is a 1D platform to build tools
A typical light source is a CO₂ laser
Combine with endoscope - new types of surgery
- Chemotherapy substitute

Why do Electrons not Fall onto a Proton in an Atom?

Uncertainty Principle

With regard to the uncertainty principle, this is an energetically unfavorable event. The uncertainty in the velocity of an electron becomes high as it approaches the proton. The kinetic energy can be high, and the electron needs to compromise in terms of position and be a particular distance from the proton.

Reference:

Solymer and Walsh. Electrical Properties of Materials, 7th Edition, p. 30

Bohr Model

In atomic physics, the Bohr model depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus — similar in structure to the solar system, but with electrostatic forces providing attraction, rather than gravity. This was an improvement on the earlier cubic model (1902), the plum-pudding model (1904), the Saturnian model (1904), and the Rutherford model (1911). Since the Bohr model is a quantum-physics based modification of the Rutherford model, many sources combine the two, referring to the Rutherford-Bohr model.

Introduced by Niels Bohr in 1913, the model's key success lay in explaining the Rydberg formula for the spectral emission lines of atomic hydrogen; while the Rydberg formula had been known experimentally, it did not gain a theoretical underpinning until the Bohr model was introduced. Not only did the Bohr model explain the reason for the structure of the Rydberg formula, but it provided a justification for its empirical results in terms of fundamental physical constants.

The Bohr model is a primitive model of the hydrogen atom. As a theory, it can be derived as a first-order approximation of the hydrogen atom using the broader and much more accurate quantum mechanics, and thus may be considered to be an obsolete scientific theory. However, because of its simplicity, and its correct results for selected systems (see below for application), the Bohr model is still commonly taught to introduce students to quantum mechanics, before moving on to the more accurate but more complex valence shell atom.

Quantum Confinement

Quantum confinement describes the increase in energy which occurs when the motion of a particle is restricted in one or more dimensions by a potential well. When the confining dimension is large compared to the wavelength of the particle, the particle behaves as if it were free. As the confining dimension decreases, the particle's energy increases. A quantum dot is a well that confines in all three dimensions such as a small sphere, a quantum wire confines in two dimensions, and a quantum well confines in one dimension.

Particle in a Box

In physical terms, the particle in a box is defined as a single point particle, enclosed in a box inside of which it experiences no force whatsoever, i.e. it is at zero potential energy. At the walls of the box, the potential rises to infinity, forming an impenetrable wall. Using this description in terms of potentials allows the Schrödinger equation to be used to determine the solution.

The quantum behavior in the box includes:

Energy quantization - It is not possible for the particle to have any arbitrary definite energy. Instead only discrete definite energy levels are allowed (if the state is not a steady state, however, any energy past zero-point energy is allowed on average).
Zero-point energy - The lowest possible energy level of the particle, called the zero-point energy, is nonzero.
Spatial nodes - In contrast to classical mechanics the Schrödinger equation predicts that for some energy levels there are nodes, implying positions at which the particle can never be found.

Solution in One-Dimension

The eigenfunction and eigenenergies of a particle of mass m in a one dimensional box of length L are

\psi _{n}={\sqrt {\frac {2}{L}}}\sin {\left({\frac {n\pi x}{L}}\right)}\,

E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,

Finite Potential Well

The finite potential well (also known as the finite square well) is a simple problem from quantum mechanics. It is an extension of the infinite potential well, in which a particle is confined to a box, but one which has finite - not infinite - potential walls. This means unlike the infinite potential well, there is a probability associated with the particle being found outside of the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy of the particle is less than potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls (because of quantum tunnelling).

Harmonic Oscillator

The quantum harmonic oscillator is the quantum mechanical analogue of the classical harmonic oscillator. It is one of the most important model systems in quantum mechanics because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point. Furthermore, it is one of the few quantum mechanical systems for which a simple exact solution is known.

Solution

|ψ_n(x)|² for the bound eigenstates, beginning with the ground state (n = 0) at the bottom and increasing in energy toward the top. The horizontal axis shows the position x, and brighter colors represent higher probability densities. In the one-dimensional harmonic oscillator problem, a particle of mass $\displaystyle m$ is subject to a potential $\displaystyle V(x)={\frac {1}{2}}m\omega ^{2}x^{2}$ . In classical mechanics, $\displaystyle m\omega ^{2}=k$ is called the spring stiffness coefficient or force constant, and $\displaystyle \omega$ the circular frequency.

The Hamiltonian of the particle is:

H={\frac {p^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}x^{2}

where x is the position operator, and p is the momentum operator $\left(p=-i\hbar {d \over dx}\right)$ . The first term represents the kinetic energy of the particle, and the second term represents the potential energy in which it resides. In order to find the energy levels and the corresponding energy eigenstates, we must solve the time-independent Schrödinger equation,

H\left|\psi \right\rangle =E\left|\psi \right\rangle

.

We can solve the differential equation in the coordinate basis, using a power series method. It turns out that there is a family of solutions,

\left\langle x|\psi _{n}\right\rangle ={\sqrt {\frac {1}{2^{n}\,n!}}}\cdot \left({\frac {m\omega }{\pi \hbar }}\right)^{1/4}\cdot \exp \left(-{\frac {m\omega x^{2}}{2\hbar }}\right)\cdot H_{n}\left({\sqrt {\frac {m\omega }{\hbar }}}x\right)

n=0,1,2,\ldots

The first six solutions (n = 0 to 5) are shown on the right. The functions $H_{n}$ are the Hermite polynomials:

H_{n}(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}

Types of Magnetic Materials

Diamagnetic

Diamagnetism is a weak repulsion from a magnetic field. It is a form of magnetism that is only exhibited by a substance in the presence of an externally applied magnetic field. It results from changes in the orbital motion of electrons. Applying a magnetic field creates a magnetic force on a moving electron in the form of F = Qv × B. This force changes the centripetal force on the electron, causing it to either speed up or slow down in its orbital motion. This changed electron speed modifies the magnetic moment of the orbital in a direction opposing the external field.

Consider two electron orbitals; one rotating clockwise and the other counterclockwise. An external magnetic field into the page will make the centripetal force on an electron rotating clockwise increase, causing it to speed up. That same field would make the centripetal force on an electron rotating counterclockwise decrease, causing it to slow down. The orbiting electrons create magnetic fields themselves, and in both cases, the change in B due to the electron's change in velocity is in the opposite direction to the external B field. Since the material originally had no net magnetic field from its orbiting electrons (because their orbits were aligned in random directions), the result is that the induced B field opposes the applied B field, and these repel each other.

All materials show a diamagnetic response in an applied magnetic field. In fact, diamagnetism is a very general phenomenon, because all paired electrons, including the core electrons of an atom will always make a weak diamagnetic contribution to the material's response. However, for materials which show some other form of magnetism (such as ferromagnetism or paramagnetism), the diamagnetism is completely overpowered. Substances which only, or mostly, display diamagnetic behaviour are termed diamagnetic materials, or diamagnets. Materials that are said to be diamagnetic are those which are usually considered by non-physicists as "non magnetic", and include water, DNA, most organic compounds such as petroleum and some plastics, and many metals, particularly the heavy ones with many core electrons, such as mercury, gold and bismuth.

Paramagnetic

Constituent atoms or molecules of paramagnetic materials have permanent magnetic moments (dipoles), even in the absence of an applied field. This generally occurs due to the presence of unpaired electrons in the atomic/molecular electron orbitals. In pure paramagnetism, the dipoles do not interact with one another and are randomly oriented in the absence of an external field due to thermal agitation, resulting in zero net magnetic moment. When a magnetic field is applied, the dipoles will tend to align with the applied field, resulting in a net magnetic moment in the direction of the applied field. In the classical description, this alignment can be understood to occur due to a torque being provided on the magnetic moments by an applied field, which tries to align the dipoles parallel to the applied field. However, the truer origins of the alignment can only be understood via the quantum-mechanical properties of spin and angular momentum.

If there is sufficient energy exchange between neighbouring dipoles they will interact, and may spontaneously align or anti-align and form magnetic domains, resulting in ferromagnetism (permanent magnets) or antiferromagnetism, respectively. Paramagnetic behavior can also be observed in ferromagnetic materials that are above their Curie temperature, and in antiferromagnets above their Néel temperature. At these temperatures the available thermal energy simply overcomes the interaction energy between the spins.

Ferromagnetic

A selection of crystalline ferromagnetic (* = ferrimagnetic) materials, along with their Curie temperatures in kelvins (K). (Kittel, p. 449.)
Material	Curie temp. (K)
Cobalt-Co	1388
Iron-Fe	1043
Magnetite-FeOFe₂O₃^*	858
Ferrite (magnet)-NiOFe₂O₃^*	858
Ferrite (magnet)-CuOFe₂O₃^*	728
Ferrite (magnet)-MgOFe₂O₃^*	713
Manganese-Mn, Bismuth-Bi	630
Nickel-Ni	627
Manganese-Mn,Antimony-Sb	587
Ferrite (magnet)-MnOFe₂O₃^*	573
Yttrium iron garnet-Y₃Fe₅O₁₂^*	560
Chromium(IV) oxide-CrO₂	386
Manganese-Mn,Arsenic-As	318
Gadolinium-Gd	292
Dysprosium-Dy	88
Europium-Eu O	69

Ferromagnetism is the "normal" form of magnetism with which most people are familiar, as exhibited in horseshoe magnets and refrigerator magnets. It is responsible for most of the magnetic behavior encountered in everyday life. The attraction between a magnet and ferromagnetic material is "the quality of magnetism first apparent to the ancient world, and to us today," according to a classic text on ferromagnetism.

Ferromagnetism is defined as the phenomenon by which materials, such as iron, in an external magnetic field become magnetized and remain magnetized for a period after the material is no longer in the field.

Physical Origin

The property of ferromagnetism is due to the direct influence of two effects from quantum mechanics: spin and the Pauli exclusion principle.

The spin of an electron, combined with its orbital angular momentum, results in a magnetic dipole moment and creates a magnetic field. (The classical analogue of quantum-mechanical spin is a spinning ball of charge, but the quantum version has distinct differences, such as the fact that it has discrete up/down states that are not described by a vector; similarly for "orbital" motion, whose classical analogue is a current loop.) In many materials (specifically, those with a filled electron shell), however, the total dipole moment of all the electrons is zero (i.e., the spins are in up/down pairs). Only atoms with partially filled shells (i.e., unpaired spins) can experience a net magnetic moment in the absence of an external field. A ferromagnetic material has many such electrons, and if they are aligned they create a measurable macroscopic field.

These permanent dipoles (often called simply "spins" even though they also generally include orbital angular momentum) tend to align in parallel to an external magnetic field, an effect called paramagnetism. (A related but much weaker effect is diamagnetism, due to the orbital motion induced by an external field, resulting in a dipole moment opposite to the applied field.) Ferromagnetism involves an additional phenomenon, however: the dipoles tend to align spontaneously, without any applied field. This is a purely quantum-mechanical effect.

Antiferromagnetic

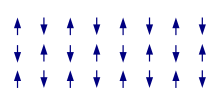
In materials that exhibit antiferromagnetism, the spins of electrons align in a regular pattern with neighboring spins pointing in opposite directions. This is a different manifestation of magnetism. Generally, antiferromagnetic materials exhibit antiferromagnetism at a low temperature, and become disordered above a certain temperature; the transition temperature is called the Néel temperature. Above the Néel temperature, the material is typically paramagnetic.

The antiferromagnetic behaviour at low temperature usually results in diamagnetic properties, but can sometimes display ferrimagnetic behaviour, which in many physically observable properties is more similar to ferromagnetic interactions.

Ferrimagnetic

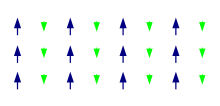
A ferrimagnetic interaction is a specific type of antiferromagnetic interaction in which the net spin of the system is not equal to zero due to the spin in each direction not being equal, and therefore not cancelling. A classic example is a dodecanuclear Manganese molecule with an effective spin of S = 10 derived from antiferromagnetic interaction on Mn(IV) metal centres with Mn(III) and Mn(II) metal centres.

Giant Magnetoresistance

Giant magnetoresistance (GMR) is a quantum mechanical effect, a type of magnetoresistance effect, observed in thin film structures composed of alternating ferromagnetic and nonmagnetic metal layers.

The effect manifests itself as a significant decrease in electrical resistance in the presence of a magnetic field. In the absence of an applied magnetic field the direction of magnetization of adjacent ferromagnetic layers is antiparallel due to a weak anti-ferromagnetic coupling between layers, and it decreases to a lower level of resistance when the magnetization of the adjacent layers align due to an applied external field. The spins of the electrons of the nonmagnetic metal align parallel or antiparallel with an applied magnetic field in equal numbers, and therefore suffer less magnetic scattering when the magnetizations of the ferromagnetic layers are parallel.

The effect is exploited commercially by manufacturers of hard disk drives. The 2007 Nobel Prize in physics was awarded to the European Albert Fert and Peter Grünberg for the discovery of GMR.

Types of GMR

Multilayer GMR

Two or more ferromagnetic layers are separated by a very thin (about 1 nm) non-ferromagnetic spacer (e.g. Fe/Cr/Fe). At certain thicknesses the RKKY coupling between adjacent ferromagnetic layers becomes antiferromagnetic, making it energetically preferable for the magnetizations of adjacent layers to align in anti-parallel. The electrical resistance of the device is normally higher in the anti-parallel case and the difference can reach more than 10% at room temperature. The interlayer spacing in these devices typically corresponds to the second antiferromagnetic peak in the AFM-FM oscillation in the RKKY coupling.

The GMR effect was first observed in the multilayer configuration, with much early research into GMR focusing on multilayer stacks of 10 or more layers.

Spin valve GMR

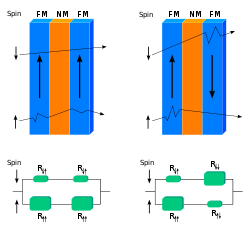
Two ferromagnetic layers are separated by a thin (about 3 nm) non-ferromagnetic spacer, but without RKKY coupling. If the coercive fields of the two ferromagnetic electrodes are different it is possible to switch them independently. Therefore, parallel and anti-parallel alignment can be achieved, and normally the resistance is again higher in the anti-parallel case. This device is sometimes also called a spin valve.

Spin valve GMR is the configuration that is industrially most useful, and is used in hard drives.

Granular GMR

Granular GMR is an effect that occurs in solid precipitates of a magnetic material in a non-magnetic matrix. In practice, granular GMR is only observed in matrices of copper containing cobalt granules. The reason for this is that copper and cobalt are immiscible, and so it is possible to create the solid precipitate by rapidly cooling a molten mixture of copper and cobalt. Granule sizes vary depending on the cooling rate and amount of subsequent annealing. Granular GMR materials have not been able to produce the high GMR ratios found in the multilayer counterparts.