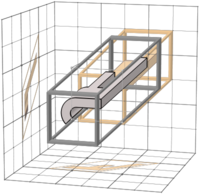
3-bit Walsh permutation

Walsh permutation

There are  A002884(3) = 4 * 6 * 7 = 168 invertible binary 3×3 matrices.

They form the general linear group GL(3,2). (As all non-zero determinants are 1 in the binary field, it is also the special linear group.)

It is isomorphic to the projective special linear group PSL(2,7), the symmetry group of the Fano plane.

Each of these maps corresponds to a permutation of seven elements, which can be seen as a collineation of the Fano plane.

six edge cases of invertibility

To be precise, the group consists of the 168 binary matrices whose inverses are integer matrices, namely with entries 0, 1 and −1. Not part of the group are the six matrices whose inverses do not contain integers: binary [[0, 1, 1], [1, 0, 1], [1, 1, 0]] [[0, 1, 1], [1, 1, 0], [1, 0, 1]] [[1, 0, 1], [0, 1, 1], [1, 1, 0]] [[1, 0, 1], [1, 1, 0], [0, 1, 1]] [[1, 1, 0], [0, 1, 1], [1, 0, 1]] [[1, 1, 0], [1, 0, 1], [0, 1, 1]] inverse [[-0.5, 0.5, 0.5], [ 0.5, -0.5, 0.5], [ 0.5, 0.5, -0.5]] [[-0.5, 0.5, 0.5], [ 0.5, 0.5, -0.5], [ 0.5, -0.5, 0.5]] [[ 0.5, -0.5, 0.5], [-0.5, 0.5, 0.5], [ 0.5, 0.5, -0.5]] [[ 0.5, 0.5, -0.5], [-0.5, 0.5, 0.5], [ 0.5, -0.5, 0.5]] [[ 0.5, -0.5, 0.5], [ 0.5, 0.5, -0.5], [-0.5, 0.5, 0.5]] [[ 0.5, 0.5, -0.5], [ 0.5, -0.5, 0.5], [-0.5, 0.5, 0.5]] The following Python script shows that the 512 binary matrices consist of 338 singular matrices, 168 with integer inverses and 6 with non-integer inverses: from itertools import product def is_integer_matrix(matrix): for row in matrix: for entry in row: if entry % 1 > 0: return False return True number_of_singular_matrices = 0 number_of_matrices_with_integer_inverses = 0 number_of_matrices_with_non_integer_inverses = 0 for m00, m01, m02, m10, m11, m12, m20, m21, m22 in product([0, 1], repeat=9): mat = np.array([[m00, m01, m02], [m10, m11, m12], [m20, m21, m22]]) try: mat_inv = np.linalg.inv(mat) if is_integer_matrix(mat_inv): number_of_matrices_with_integer_inverses += 1 else: number_of_matrices_with_non_integer_inverses += 1 except np.linalg.LinAlgError: number_of_singular_matrices += 1 print('singular matrices:', number_of_singular_matrices) print('matrices with integer inverses:', number_of_matrices_with_integer_inverses) print('matrices with non-integer inverses:', number_of_matrices_with_non_integer_inverses)

Representations

overview

These images show the connection between the 3×3 matrices and the permutations: Each row of the 3×3 matrix can be interpreted as a number in $\{1..7\}$. The corresponding Walsh function (row of a Walsh matrix) is shown to its right. The columns of the resulting 3×8 matrix can be interpreted as a permutation of $(0..7)$. (The small gray cube shows the result of applying the permutation. Reading it as a sequence corresponds to reading the permutation matrix by rows.) 124 471 456 316 341

permuted Walsh matrices
These images show why the author chose the term Walsh permutation. A permutation is Walsh iff applying it to the columns of a Walsh matrix creates a matrix that can also be described as a Walsh matrix with permuted rows.

transformations (letter compound)
Here the binary 3×3 matrices are used as transformation matrices. A list of these files can be found here. as inverses These are transforms with inverses of binary matrices, which contain some negative 1s. A list of these files can be found here.

transformations (colored cube)

These images show the connection between transforms and permutations: The vertices of the periodic gray cubes have values from 0 to 7, and the transformation moves each vertex of the colored cube to some vertex in some gray cube. This file shows essentially the same as this one (shown below), but the colored small vertices make it clearer how it corresponds to this. (This is the result of applying the permutation. It corresponds to the gray cube in the overview files above.) as inverses

cube with RGB vertices and complement patterns
The colors are in the same vertices of the gray cube as in the transform images above. This is the result of applying the permutation. The number values of the colors are like those in the gray cubes in the overview files (in the first box above). Complementary vertices are connected by brown edges. The patterns are numbered 1..7. 7 2 7 4 6

Conjugacy classes

The group has  A006951(3) = 6 conjugacy classes. They almost correspond to the cycle type,
but there are two different conjugacy classes with 7-cycles. (For the distinction between them, see here.)

The permutations in 2+2 are self-inverse, and their fixed points correspond to Walsh functions. They can be found here.

more examples
description	neutral	2+2	2+4	3+3	7a	7b
size	1	21	42	56	24	24
examples	124	421	136	241	765	357
		623	247	517	512	243

The 3×3 matrices in the same conjugacy class are similar.

examples of matrix similarity
$P^{-1}$	$A$	$P$	$=$	$B$	matrix multiplication
127	461	127	$=$	753
147	461	172	$=$	753
751	461	436	$=$	753
731	461	463	$=$	753

Cycle shapes

In a symmetric representation like the Fano plane, there are 33 different cycle shapes (or 24 if the direction is ignored).
A complete list can be found here. They are denoted by city names, followed by a qualifier of the direction, where needed.

triangle Berlin
217 742 471

hexagon Shanghai
236 362 315 546 531 465

triangles Santiago + and −
Inverse 3×3 matrices differ in their determinant. Those in the inner triangle have 1, and those in the outer have −1. 567 735 657 753 673 376

hexagons Buenos Aires 5 and 6
Inverse 3×3 matrices differ in their number of ones. Those in the inner hexagon have 5, and those in the outer have 6. 175 574 165 534 726 327 526 325 364 136 764 137

$A$ and $B$ have the same cycle shape, if there is a $P$ from the symmetric subgroup, so that $B=P^{-1}AP$. (The 3×3 matrix of $P$ is a permutation matrix.)

This is a refinement of matrix similarity, where $P$ is allowed to be any element of the group. (Cycle shapes are a refinement of conjugacy classes.)

Powers and cycle graph

The cycle graph of this group has 28 triangles, 21 squares and 8 heptagons.

Each of the following rows is an example of a cycle. (Each one is closed by the neutral element, which is not shown.)
It shows consecutive powers of the first element from left to right. (Also of the last element from right to left.)
Elements in symmetric positions are inverse to each other.

Triangles

Each of the 28 triangles contains two inverse permutations of cycle type 3+3.

Squares

This shows why there are two permutations of cycle type 2+4 for each one with 2+2.

Heptagons

Alexandria, Tripoli, Cairo
713 576 452 341 637 265 Alexandria a Tripoli a Cairo b Cairo a Tripoli b Alexandria b

Tripoli, Cairo, Alexandria
763 251 647 532 416 375 Tripoli b Cairo b Alexandria a Alexandria b Cairo a Tripoli a